Thermal Contact Between Plain Plates

Consider the problem of the steady heat flux in the complex plate with width ∑hi  and thermal conductivity coefficients ki, whose first and last surface maintain temperatures t1 and tn+1 and between the plates with numbers m-1 and m+1, there is a thermal contact with specific resistance Rm(see figure).

 

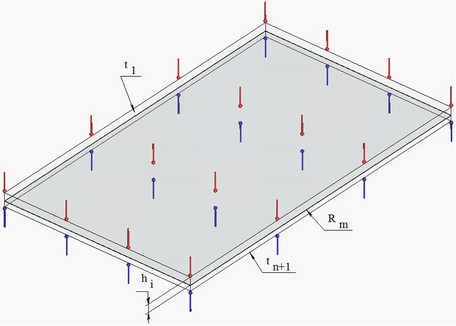
The temperature change and heat flux along the width of the complex plate, consisting of n sheets with widths h1, h2,... hn and thermal conductivity coefficients k1, k2,... kn , respectively, for each sheet, fi, i=1,2,..., n are defined using the formula:

Let all sheets, save two ones, are in the ideal thermal contact along boundary surfaces. Put thermal resistance Rm between sheets numbered m-1 and m+1, then the heat flux will be uninterrupted at the transition from one area to the other, and in this case, will be the same in each point (i.e. f1=f2=...=fn=f). The change of temperature between the opposite surfaces of the entire complex plate will equal the sum of temperature changes in separate sheets:

Then:

,

 

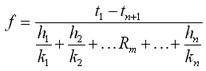
Let accept the following initial data: number of sheets is n=2 , length and width of each sheet are 100 mmand 50 mm respectively, and widths of the sheets h1, h2 , are 8 mm, 10 mm . The applied temperatures t1and t2 equal 373K and 273K respectively.

Thermal conductivity coefficients are:

,

Thermal resistance of the contact

(it is approximately equivalent to the thermal resistance of the plain air layer with the width 0.05 mm with

)

Thus,
.

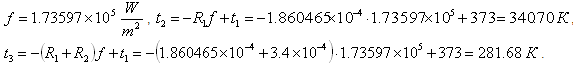
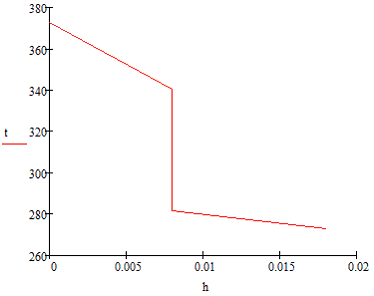
By calculation with the help of AutoFEM Analysis, we have obtained the following results (for the lower and upper sides of the contact, respectively):

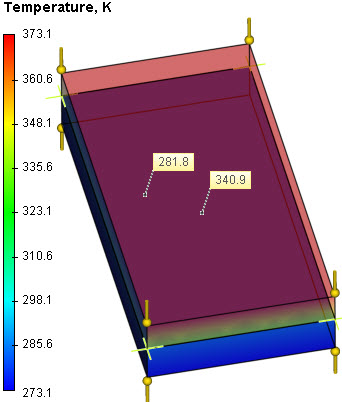
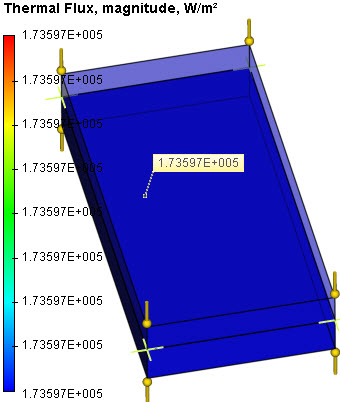
Table 1*

Table 2*

 

 

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.

 

Read more about AutoFEM Thermal Analysis

autofem.com

Return to contents