Contact Between a Cylindrical Bar and a Ring

Let us consider the contact between the cylindrical bar and the ring (see figure). It is supposed that the parts are not tied together. Each part can freely moves by the other one (without friction).
The normal force P is applied to free ends of the ring. The magnitude of the force is 1E+005 N .

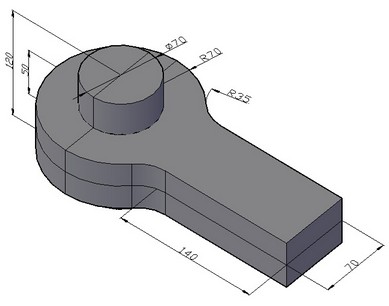
Let us use the following initial data: the diameter of the cylindrical axis d is 0.07 m, the length of the axis H is 0.12 m, the outer radius of the eye ring R is 0.07 m, the thickness h of the eye ring is 0.05 m, the width of the belt of the eye ring b is 0.07 m, the length of the belt of the eye ring L is 0.14 m, the transition radius of the eye ring r is 0.035 m.
Material properties are the Young's modulus E = 2.1E+011 Pa and Poisson's ratio ν = 0.28.
The normal stress into belt section can be calculated using the following semi empirical formula:

σ = k*P / h*(2*R - d)

where P is the normal force, k is the stress concentration factor (k = 3.6).
The calculation using the above mentioned formulas gives the result: σ = 1.0286E+008 Pa.
After carrying out calculations by the AutoFEM Analysis the following results are obtained: the normal stress σX ranges from 0.8E+008 Pa to 0.99E+008 Pa. Let us compare σX with σ:

Table 1.Parameters of the finite element mesh

Table 2.The result “Normal stress OX”*

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.

 

Read more about AutoFEM Static Analysis

autofem.com

Return to contents