Axial and Transverse Vibration Frequency of a Beam with a Weight

Let us consider the cantilever beam, the right end of which is under the weight.

The length of the beam is L. The beam cross-section is a rectangle of width b and height h. The mass of the weight is M. The specific mass of the beam is m.
m = ρ F,
where F = b h, ρ is the density of the material of the beam.

Let L is equal to 0.5 m, b is equal to 0.02 m, h is equal to 0.05 m.
The material properties are: the Young's modulus E = 2.1E+011 Pа, Poisson's ratio ν=0.28, the density ρ = 7800 kg / m3.
The mass of the weight M is equal to 2.m.L kg (i.e. 7.8 kg).
Analytical solution of this problem is given by the following formulas:
a) the axial vibration frequency

b) the transverse vibration frequency
,
.
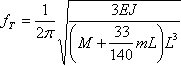Thus, fA = 1078.962 Hz , fT = 22.092 Hz.

After carrying out calculation with the help of AutoFEM, the following results are obtained:

Table 1. Parameters of finite element mesh

Table 2. Result "Frequency"*

Conclusions:

The relative error of the numerical solution compared with the analytical solution not exceed 0.7%.

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.

 

 

Read more about AutoFEM Frequency Analysis

autofem.com

Return to contents