Bending of a Simply-Supported Beam Under Impact in the Middle

Let us consider a simply-supported beam of L length on which the burden of M mass falls from the H height and impacts in the middle. Beam cross-section is a rectangle of b width and h height. We can neglect the beam mass.

Bending of a Cantilever Beam under a Concentrated Load

It is necessary to define the beam maximum bending.

Let us consider L=1000 mm, b=50 mm, h=20 mm. The material properties are set by default. Modulus of elasticity E = 2E+011 Pa, Poisson ratio v = 0.29. The mass of burden is M = 79.42 kg. The height of burden fall is H = 4.0 mm.

Create Transitional processes study. The displacement of the lower edge of the left butt end is restricted by Z axis, the lower edge is fixed for the right butt. The load Acceleration of gravity is applied to the burden (as the beam mass can be neglected). The initial velocity of 280.1428 mm/s that corresponds to 4 mm of fall height is applied to the burden.

Bending of a Cantilever Beam under a Concentrated Load, the finite element model with applied loads and restraints

The finite element model with applied loads and restraints

An analytical solution is the following:

where - a moment of inertia of the section.

Let us find the step on which the maximum deviation by graph appears after calculation using AutoFEM Analysis:

Bending of a Cantilever Beam under a Concentrated Load, Result "Displacement, magnitude" of finite element analysis

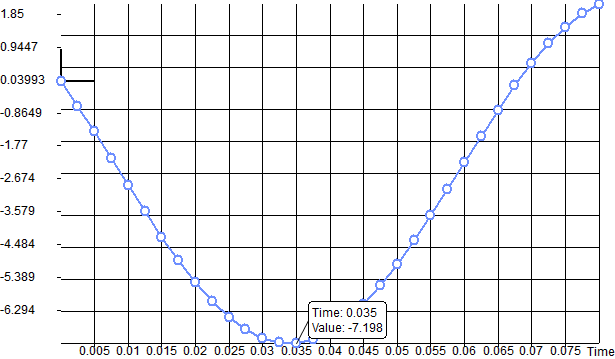
After carrying out calculation with the help of AutoFEM, the following results are obtained:

Table 1.Parameters of the finite element mesh

Finite Element Type	Number of Nodes	Number of Finite Elements
quadratic tetrahedron	3209	9944

Table 2.Parameters of temporal discretization

Total calculation time (s)	Time step (s)	Number of time layers
0.08	0.0025	32

Table 3. Result "Displacement, OZ"*

Numerical Solution Displacement OZ w*, mm	Analytical Solution Displacement OZ w, mm	Error δ =100%* \|w* - w\| / \|w\|
7.198	7.2103	0.17

Conclusions:

The relative error of the numerical solution compared to the analytical solution is equal to 0.17% for quadratic finite elements.

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.