Disk Having a Constant Temperature on the External Cylindrical Surface and Being Heated along the Axis (surface)

Disk Having a Constant Temperature on the External Cylindrical Surface is being heated along the axis

Let us consider a two-dimensional problem of a steady-state temperature distribution on the end-face cross-section of a disk. A heater of zero thickness (a line) with a power of P=100 W is situated on the axis of the disk, and on the periphery a constant temperature of 273.15 oK is held.

Parameters of a disk: metal disk with thickness d=5 mm, radius R=100 mm and thermal conductivity K=50 W/(m • oK) [Alloy Steel (SS)].

(see figure).

Solution of this problem in which the source is regarded as distributed can be obtained by solving the problem for a point source of the heat. Let the origin of the coordinate system coincide with the center of the circular surface of a disk. The differential equation that has to be solved for a point source has the form:

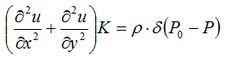
where ρ – density of a distributed heat source. For our case: ρ = P / d. Solution of this equation is a Green’s function G (heat source function)

In this solution the zero point corresponds to the center of the disk. The Z-axis of the coordinate system, in which the solution is sought, is directed along the axis of the disk.

Steady-State Temperature of a Multilayer Wall, the finite element model with applied temperatures

The finite element model with applied boundary conditions

Let us compare analytical solution with the solution obtained from AutoFEM. After carrying out calculation the following results are obtained:

Table 1. Parameters of finite element mesh

Finite element type	Number of nodes	Number of finite elements
linear tetrahedron	3405	6608

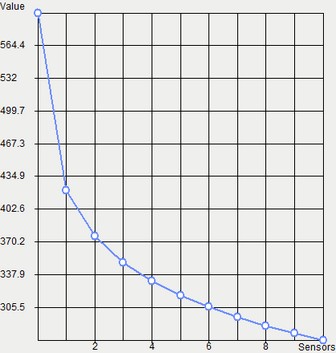
Table 2. Result "Temperature"

Distance from the center, mm	Numerical solution Temperature T*, K	Analytical solution Temperature T, К	Error δ = 100%* \|T* - T\| / \|T\|
R 30	349.9436	349.7972	0.04
R 40	331.5504	331.4828	0.02
R 50	317.3002	317.2771	0.01
R 60	305.6999	305.6701	0.01

Steady-State Temperature of the Multilayer Wall, temperature distribution

Conclusions:

Relative error of the numerical solution as compared to the analytical solution did not exceed 0.04% when using linear element. Accuracy of the calculation grows when moving away from the heat source because of the singularity of the analytical solution at the point of heat source application (at the center of a disk).

The plot of dependence of the temperature on the radius shows that analytical and numerical solutions practically coincide. This implies that distributions of temperature maximums and minimums are the same, and hence, calculation of thermal heat fluxes and power will be carried out with the same degree of accuracy.

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.

autofem.com

Return to contents