Large Deflection of a Circular Plate

Large Deflection of a Circular Plate Under a Uniformly Distributed Load

Let us consider a circular plate with the radius a and the thickness h. The plate is clamped and subjected to a uniformly distributed load with the intensity q (see figure).

The finite element model of a clamped circular plate under a uniformly distributed load

The finite element model of a clamped circular plate under a uniformly distributed load (large deflection)

Let us use the following initial data: the radius of the plate a is 0.25 m, the thickness of the plate h is 0.005 m, the load intensity q is 1E+05 Pa.
Material properties are E=2.1E+011 and ν= 0.28.

Let us use the following approximate formula to calculate displacements of the plate center:
,
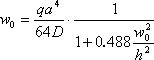where

is the bending stiffness of the plate.

Solving this equation for w0, we obtain the value of the maximum deflection, which is expected in the center of the plate: w0= 2.3258E-003 m.

After carrying out calculations (taking into account nonlinearity) by the AutoFEM Analysis the following results are obtained:

Table 1.Parameters of the finite element mesh

Finite Element Type	Number of Nodes	Number of Finite Elements
Quadratic tetrahedron	3000	8601

Table 2.The result “Displacement, magnitude”

Numerical solution Displacement w0*, m	Analytical solution Displacement w0, m	Error δ =100%\|w0- w0\|/\| w0 \|
2.2946E-003	2.3258E-003	1.34

Large Deflection of a Circular Plate Under a Uniformly Distributed Load, the result “Displacement, magnitude”

Conclusions:

The relative error of the numerical solution compared to the analytical solution is equal to 1.38% for quadratic finite elements.

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the tables.