 |
AutoFEM Analysis Buckling Analysis | ||||||
Equilibrium of a statically loaded structure is called stable, if small disturbances cause small deformations. In certain cases of loading structures, situations are possible that are called buckling – when small disturbances from the forces applied to the system cause large structural deformations, which exceed those defined within the framework of the linear theory of elasticity. Loads that cause buckling are called critical, and the respective states – critical states. Under compressing forces, which even insignificantly exceed the critical value, additional bending stresses reach quite large values and directly threaten structural integrity. Therefore, the critical state which immediately precedes rupture, is considered inadmissible in real-life conditions. The threat of buckling is especially great in compressed zones for light thin-wall structures, such as slender rods, plates and shells. The buckling phenomenon exhibits various forms: completely new forms of equilibrium appear; known stable configurations deteriorate, etc.
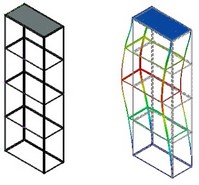
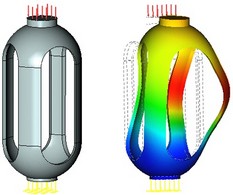
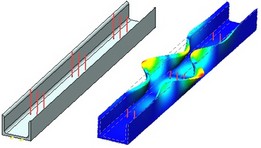
The buckling analysis module serves for conducting the so-called initial buckling structural study. The result of the study is a coefficient of the critical load, under which the structure may spring into a new equilibrium state, and the shape of the new equilibrium state corresponding to that load. In such a case, a situation is possible, when the critical load, under which buckling occurs, could be much less than the load, under which the maximum strength of the structure will be exceeded based on the linear static stressed state of the structure. In other words, the stresses in the structural material may not reach the ultimate values, but deformations due to buckling may cause structural rupture. Therefore, the buckling condition can be formulated based on the critical load criterion as follows:
Actual loads applied to a structure, must be less than the estimated critical load, subject to an asserted safety factor:
|
Having estimated the value of the critical load, under which the structure may buckle, you can optimize the part in order to achieve the safe condition. For example, for a slender object, you can increase resistance to buckling by reducing the length or increasing the thickness of your object, or create additional ribs for rigidity.