 |
AutoFEM Analysis Erzwungene Oszillationsanalyse | ||||||
Harmonikale Erzwungene Oszillation
Die Analyse der Oszillation wird zur Vorhersage des Verhaltens einer Struktur unter externen Ereignissen im Zusammenhang mit dem harmonikalen Gesetz. Diese Ereignisse schließen Kräfte und/oder kinematische Anregungen ein. Zusätzlich können die Auswirkungen der Systemdämpfung berücksichtigt werden.
Das Ziel der erzwungenen Oszillationsanalyse ist es, die Abhängigkeit der Antwort des Systems auf die Frequenz von zwingenden Aktionen zu erhalten. Als Resultat werden Amplituden der Verschiebungen, die Vibrationsbeschleunigung und Vibrationsüberlastung berechnet, welche durch die vorgegebenen Frequenzen entstehen. Entsprechend kann für einen Frequenzbereich die Abhängigkeiten der Amplituden und Vibrationsbeschleunigungen berechnet werden, was wichtig ist für die Vibrationsstabilität eines Systems im vorgegebenen Frequenzbereich.
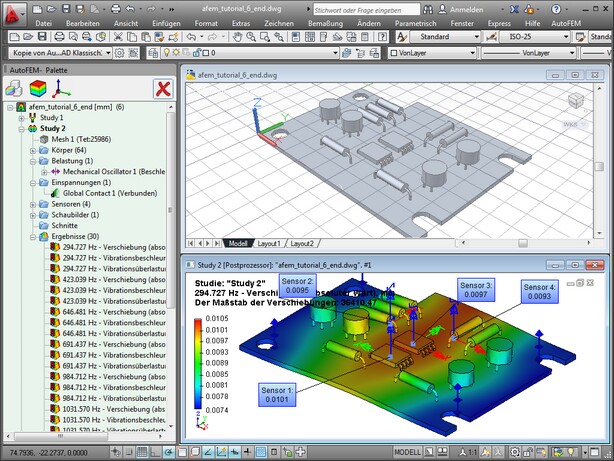
Einführung
Das Modul "Erzwungene Oszillationen" von Finite-Elemente-Systeme von AutoFEM Analyse, kann zur Analyse von erzwungen Oszillationen der folgenden Typen verwendet werden:
| • | Erzwungene Oszillationen des Systems ohne Berücksichtigung der Dämpfung unter der harmonikalen Kraft. Im System mit vielen Freiheitsgraden werden diese Oszillationen mit der folgenden Gleichung beschrieben: M : symmetrische quadratische Matrix der Masse; K : symmetrisches Quadrat Steifheitsmatrix des Systems; F0 : Vektor der Amplituden der zwingenden Wirkung; ω : Frequenz der zwingenden Wirkung; u, u'' : sind Vektoren von Koordinaten von Systempunkten, die ihre Position in der Zeit t und deren Beschleunigung ändern; φ : die erste Phase des Erregers. |
| • | Erzwungene Oszillationen des Systems mit Berücksichtigung der Dämpfung unter der harmonikalen Kraft. Diese Oszillationen werden mit der folgenden Gleichung beschrieben: |
![]()
| • | C ist die symmetrische quadratische Matrix der Dämpfung und u' ist der Vektor der Geschwindigkeit der Systempunkte. Wir gehen davon aus, dass das System in Übereinstimmung mit Rayleigh Gesetz gedämpft wird, d.h. sie ist proportional zur Verteilung von Steifheit und Masse des Systems und mit der folgenden Gleichung beschrieben: |
![]()
wobei a ein Verhältnis von Masse und b ist ein Aspekt-Verhältnis von Steifheit ist. (beide Verhältnisse skalare sind).
| • | Erzwungene Oszillationen der beiden oben erwähnten Typen von Systemen, entstehen aus der Bewegung durch das harmonikalische Gesetz. Das heißt eins oder mehrere Systeme führen zu Oszillationsverschiebungen. Differentialgleichungen, die diesen Typ beschreiben sind analog zu den oben erwähnten, aber unterscheiden sich in der harmonikalen Zwangskraft, welche durch die folgende Formel beschrieben wird: |
| • |
Einige Zwangskräfte oder/und Verschiebungen können auf das System wirken, aber ihre Frequenz muss gleich sein
Die Rotation einer Welle oder Spindel in einem Ungleichtgewichtszustand auf elastischen Stützen kann als Beispiel der harmonischen Zwangskraft dienen. Kinematische Erregung wird angewendet, wenn die Werte der Zwangskräfte nicht bekannt sind, im Gegensatz zu den Amplituden der Oszillationen einiger Strukturelemente, die bekannt sind.
Der Prozess der Energieverlustes der mechanischen Oszillation, welcher zur schrittweisen Abschwächung der pauschal produzierten Oszillation des Systems führt, wird als “Dämpfung” bezeichnet. Dämpfende Kräfte können verschiedene Ursprünge haben, nämlich: die Reibung zwischen trockenen Flächen, Reibung zwischen geschmierten Flächen, interne Reibung, Luft- oder Wasserwiderstand usw. Es wird in der Regel angenommen, dass die dämpfenden Kräfte proportional zur Geschwindigkeit (visköse Dämpfung) auftreten. Alle Widerstandskräfte werden durch äquivalente Dämpfungskräfte ersetzt ausgehend von der Gegebenheit, dass sie pro Zyklus gleich viel Energie abbauen wie echte Kräfte.
Die Gleichung von erzwungenen Oszillationen mit der Berücksichtigung von Dämpfung i th Masse, was die Lösung der vorherigen Differentialgleichungen ist, ist folgend:
![]() ,
,
ω0 ist die Winkelfrequenz der Dämpfung
ω ist die Winkelfrequenz der Zwangskräfte
2n=c/m ,
wobei ci der Dämpffaktor für den Modus i th ist; und mi die Masse.
Es besteht aus zwei Teilen: Der Ausdruck in Klammern beschreibt die abschwächenden Oszillationen bei der Dämpfungsfrequenz die leicht Unterschiedlich der Frequenz der freien Oszillationen ist; Der Rest entspricht der erzwungenen Oszillationen mit der Frequenz ω.
Um die Auswirkungen der Dämpfung zu klären, betrachten wir das Diagramm der Abhängigkeit des Verstärkungsfaktors der Amplituden :

Auf der Rate der Frequenzen von erzwungenen und freien Oszillationen ω/ω0 mit verschiedenen Werten des Dämpfungsfaktors γ=n/ω=c/ccritical , wobei ccritical der kritische Faktor der viskösen Dämpfung ist, bei welcher die Oszillationen nicht stattfinden.

Die Grafik zeigt, dass wenn die Frequenz der erzwungenen Oszillation tief im Vergleich mit den Eigenfrequenzen von freien Oszillationen ist, die Verschiebung der Punkte des Systems ungefähr gleich der Verschiebung bei statischer Belastung durch Zwangskräfte sind. Wenn die führende harmonikale Kraft eine hohe Frequenz hat, dann wird unabhängig vom Dämpffaktor keine erzwungene Oszillation eines Systems stattfinden, welches eine tiefe Eigenfrequenz hat. In beiden Fällen:ω<<ω0 und ω>>ω0, hat die Dämpfung keinen Einfluß auf die erzwungenen Oszillationen, wenn aber die Rate der oben erwähnten Frequenzen ungefähr 1 sind, wird die Dämpfung signifikante Auswirkungen auf den Verstärkungsfaktor haben. Bei einem kleinen Dämpffaktor, ist der größte Einfluß der Dämpfung nahe der Resonanzfrequenzen. Dies zu berücksichtigen ist wichtig, wenn Strukturen Analysiert werden. Zur Analyse der erzwungenen Oszillationen einer Struktur nahe der Eigenfrequenzen, der Import der Werte der Eigenfrequenzen aus den Resultaten der Berechnung der Frequenzanalyse möglich (siehe unten).
Der Dämpffaktor γj für j th Modus ist verbunden mit dem Aspektverhältnis a, b durch folgende Gleichung:
![]() .
.
Der Wert des Dämpfungsfaktors γ kann Werte von 0.01 für schwach gedämpfte Systeme (ganzmetall Objekte); 0.02-0.04 (Metallstrukturen mit permanenten Befestigungspunkten, welche sich nur unter der Streckgrenze verformen); 0.03-0.07 (Metallstrukturen mit in-cut-Verbindungen); 0.05 für Gummi; und bis 0.15 für stark gedämpfte Systeme
Wenn die Dämpfungsfaktoren für i th und j th Modi bekannt sind, wird das Aspektverhältnis mit folgenden Formeln berechnet:
![]() ,
,
![]() .
.
Falls der Koeffizient a gleich null ist, wird die Dämpfung relativ genannt und der Dämpfungsfaktor wird für j th Modus proportional zur Winkelfrequenz des Modus ohne Dämpfung sein. Folglich mildern sich Oszillationen die höheren Modi entsprechen schneller.
Falls der Koeffizient b gleich null ist, wird die Dämpfung absolut genannt und der Dämpfungsfaktor für j th Modus wird umgekehrt proportional zur Winkelfrequenz dieses Modus ohne Dämpfung sein. Folglich mildern sich Oszillationen die tieferen Modi entsprechen langsamer.
Die Hauptresultate der Berechnung der Module der erzwungenen Oszillationen sind folgende Werte:
| • | Amplituden der Verschiebung der Finite-Elemente-Netz Knoten Um; |
| • | Vibrationsbeschleunigungen der Finite-Elemente-Netz Knoten, ausgedrückt in Amplituden: Um als U''m=Umω2 ; |
| • | Vibrationsüberlastungen, definiert als die Rate der Vibrationsbeschleunigung zum freien Fall U''m/g. |
Berechnung der erzwungenen Oszillationsanalysen
| 1. | Erstellung der "Studie". Wenn Sie eine Studie erstellen, wählen sie den Typ "erzwungene Oszillationsanalyse" Es ist möglich eine Studie des Typs "Frequenzanalyse zu kopieren und deren Typ zu ändern; In diesem Fall wird das Netz und die Randbedingungen übertragen. |
| 2. | Material wählen. Um das Material zu wählen ist es nötig mit einem Rechtsklick auf den Ordner "Körper" das Kontextmenü zu öffnen und dann “Material” zu wählen. |
| 3. | Randbedingungen festlegen. In der Analyse der erzwungenen Oszillationen, wie in der statischen Analyse, stellen Fixierungen und Belastungen die Randbedingungen dar. In dieser Art von Studie können alle Arten von Fixierungen und Belastungen eingesetzt werden, deren Einsatz ist zwingende Voraussetzung für eine korrekte Berechnung. Die Beschränkungen der Bewegung des Körpers können die Bedingung erfüllen. Für die statische Analyse, muss das Modell Fixierungen haben, welche verhindern, dass es sich frei im Raum bewegt. Wird diese Bedingung nicht erfüllt, führt dies zu einer falschen Berechnung der Finite-Elemente-Modells oder zu einem Abbruch der Berechnung. Die kinematische Last "Oszillator" kann partielle oder totale Fixierungen ersetzen. |
| 4. | Frequenzen und Dämpfung festlegen. Vor der Ausführung der Berechnung muss der Nutzer die Frequenzwerte der Belastungen, für welche die Analyse der erzwungene Oszillation durchgeführt wird, sowie die Dämpfungswerte. |
| 5. | Analyse der Resultate. Um die angezeigten Resultate zu personalisieren, können Sie einen Rechtsklick auf den Ordner "Resultate" im Studienbaum und "Resultate" selektieren. Die Resultate der erzwungenen Oszillationsanalyse sind: Amplituden der Verschiebungen, Vibrationsbeschleunigungen oder Vibrationsüberlastungen, Oszillationsphasen. Für jeden Resultatetyp, gibt es die Möglichkeit, das deformierte Objekt in den verschiedenen Phasen anzuschauen. |
Installationspezifische Einstellungen des Preprozessors in der erzwungenen Oszillationsanalyse
| 1. | Restriktionseinstellungen. Das Modell kann durch partielle oder totale Restriktionen limitiert sein. Wenn partielle Restriktionen gewählt sind, sind die Einstellungen der Bewegung andere als null verboten. |
| 2. | Kräfteeinstellungen. Um die Amplituden der Kräfte einzurichten die folgenden Typen von Kräfte können auf die Oberflächen, Kanten oder Punkte angebracht werden (Beschleunigung kann auf den ganzen Körper angebracht werden): |
| • | Kraft; |
| • | Druck; |
| • | Beschleunigung; |
| • | zylindrische Belastung |
| • | Drehkraft. |
Eine Mehrzahl an Belastungen können gleichzeitig auf den Körper einwirken, aber alle davon müssen die gleiche Frequenz haben. Für jede erlaubte Belastung kann die eigene Anfangsphase der Oszillation eingestellt werden.
| 3. | Kinematische Belastungseinstellungen (Oszillator). Um die Oszillationsamplitüde für die Abstützung einzustellen, müssen die Oszillatorbelastungen auf Elemente des Modells angebracht werden. Die Last kann auf Oberflächen, Kanten oder Punkte des Körpers, sowie auf ganze Körper angewandt werden. Um die Richtung anzugeben, muss der Oszillations LCS selektiert werden und die Richtung angegeben werden, die der relevanten LCS Achse entspricht. Der Typ der kinematischen Belastung wird aus dem Aufklappmenü gewählt und kann einer der folgenden sein: |
| • | Amplitude der Punktverschiebung; |
| • | Geschwindigkeit; |
| • | Beschleunigung; |
| • | Überlastung. |
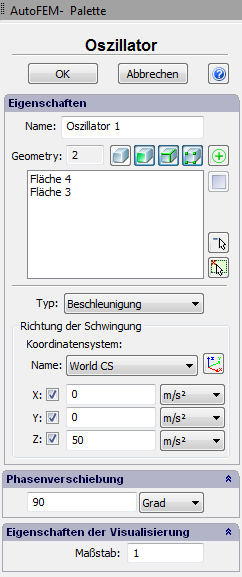
In dem separaten Bereich, kann man die Phasenverschiebung einstellen, entweder in Grad oder Bogenmaß.
Bei der Kombination der Oszillatorlast und partiellen Fixierungen, Richtungen der Oszillationen und Limitierungen müssen unterschiedlich sein für ein einzelnes Element des Modells.
Einstellung des Prozessors der erzwungenen Oszillationsanalyse
Unter [Allgemein] können sie die deskriptiven Eigenschaften der Studie definieren oder anpassen: Name, Typ, und Kommentare.
Unter [Parameter], ist es möglich die Frequenzen der externen Belastungen und die Parameter der Rayleigh Dämpfung einzustellen.
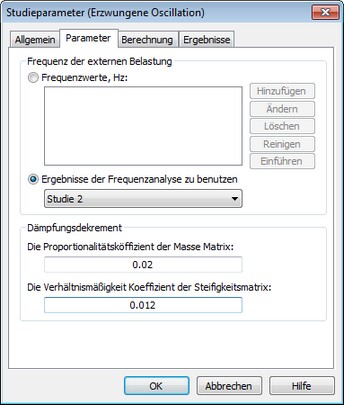
In der Gruppe "Frequenzen der externen Belastungen", können Frequenzen zugehörig zu ausgewählten externen Belastungen eingeführt werden. Es gibt mehrere Wege diese Werte einzufügen:
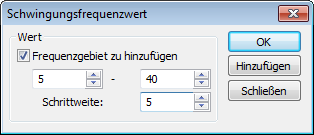
| 1. | Der Knopf [Hinzufügen] erlaubt das hinzufügen vom einzelnen Wert der Frequenz oder einen Frequenzbereich einzufügen, bei welchem Anfangs- und Endwert, sowie die Schritte angegeben werden können. |
| 2. | Der Knopf [Einführen] öffnet das Dialogfenster, wo Werte der Resonanzfrequenzen aus den Resultaten von früheren Studien importiert werden können. |

| 3. | Wenn es nötig ist, die erzwungenen Oszillationen nur bei allen Resonanzfrequenzen, die in früheren Analysen berechnet wurden, sollten Sie das Element "Benutzen früherer Analyseresultate" benutzen. Dort kann die Assoziative Verbindung mit den Resultaten der ausgewählten Studie hergestellt werden. Die Werte werden aktualisiert und automatisch für die erzwungene Oszillationsanalyse benutzt |
Ober der Liste der Frequenzwerte können folgende Einstellungen vorgenommen werden:
| • | [Ändern] erlaubt es einzelne Werte neu zu definieren |
| • | [Löschen] löscht die ausgewählte Frequenz aus der Liste |
| • | [Reinigen] Entfernt die ganze Liste von Frequenzwerten. |
In der Gruppe der Parameter "Rayleigh Dämpfung, werden die Werte der Dämpfungsfaktoren der Struktur a und b definiert.
| • | [Lösen] erlaubt es die Prozessoreigenschaften für die Lösung der Gleichungssysteme einzustellen. Die Einstellungsparameter sind ähnlich zu denen der statischen Analyse. |
| • | [Ergebnisse] ermöglicht die Wahl der Typen von Resultaten die nach der Berechnung angezeigt werden sollen. |
Postprozessor Eigenschaften und Analyse der Resultate der erzwungenen Oszillationsanalyse
In [Ergebnisse], kann man die folgenden Typen von Ergebnisse in Gruppen organisiert sehen:

Die Gruppe Belastungen enthält folgende Resultate:
Komponenten, die auf der Finite-Elemente-Modell angewandt sind und das Modul der Lasten reduziert zu Knoten. Diese Art der Ergebnisse dient als Referenz.
Die Gruppe Verschiebungen enthält folgende Resultate:
| • | Verschiebungen von Punkten des Finite-Elemente-Modell mit der Berücksichtigung der Phasenverschiebung relativ zu der Phase des Erregers in der Richtung der Achsen des globalen Koordinatensystem (CS): |
![]() ,
, ![]() ,
, ![]() ,ebenso wie das Verschiebungsmodul
,ebenso wie das Verschiebungsmodul ![]() .
.
| • | Tatsächlicher Anteil der Verschiebungen in Richtung der Achsen des globalen CS: Re(UX), Re(UY), Re(UZ), sowie das Modul des tatsächlichen Anteil der Verschiebungen |
| • | Virtueller Anteil der Verschiebungen in Richtung der Achsen des globalen CS: Im(UX), Im(UY), Im(UZ), sowie das Modul des virtuellen Anteil der Verschiebungen |
| • | Amplitude der Verschiebungen der Punkte des Finite-Elemente-Modells (ohne Berücksichtigung der Phasenverschiebung relativ zu der Phase des Erregers) in Richtung der Achsen des globalen CS: UXm, UYm, UZm, sowie das Amplitudenmodul |
| • | Phasenwinkel für Verschiebungskomponente der Punkte des Finite-Elemente-Modells in Richtung der Achsen des globalen CS relativ zu der Phase des Erregers: |
Im Fall dass die Phasenverschiebung vorgegeben ist, können Sie separate Diagramme für die tatsächlichen und virtuellen Komponenten der Verschiebung erhalten, sowie die absoluten Werte der Phasen in den Punkten des Finite-Elemente-Modells.

In der Gruppe Vibrationsbeschleunigung können sie die Ableitung der Amplitudendiagramme der Vibrationsbeschleunigung im Bezug auf die Punkte des Finite-Elemente-Modells sehen U''m=Umω2 . Die Vibrationsbeschleunigungsphase unterscheidet sich um 180 (π rad) von der Verschiebungsphase.
In der Gruppe Vibrationsüberlastung können Sie die Ableitung der Diagramme der Vibrationsüberlastung U''m/g, gemessen in Bezug auf die Beschleunigung des freien Falls sehen.
So kann das Diagramm des Ergebnisses angezeigt werden.
