|
AutoFEM Analysis Forced Oscillation Analysis | ||||||
Oscillazioni Armoniche Forzate
L'Analisi di oscillazioni armoniche forzate viene eseguita per prevedere il comportamento di una struttura sotto azioni esterne che cambiano secondo la legge armonica. Queste azioni includono la forza e/o di eccitazione cinematica. In aggiunta ad esso, l'impatto dello smorzamento sistema può essere preso in considerazione.
L'obiettivo dell'analisi delle oscillazione forzate è quello di ottenere una dipendenza della risposta del sistema sulla frequenza delle azioni avvincenti. Come risultato dei calcoli otteniamo ampiezze di spostamenti, vibrazioni, e sovraccarichi da vibrazione alla frequenza di azioni avvincenti preimpostate. Secondo questi risultati, si può ottenere, per un intervallo di frequenza, le dipendenze di ampiezze e vibrazione alla frequenza di azioni avvincenti, che è importante con la valutazione della stabilità di vibrazione del sistema in questa gamma di frequenze preselezionate.
Introduzione
Il modulo "Forced oscillazioni" del sistema modellazione agli elementi finiti, Analysis AutoFEM, possono essere utilizzati per analizzare le oscillazioni forzate stabiliti dei seguenti tipi:
| • | oscillazione del sistema forzato senza conto smorzamento sotto l'azione della forza attrattiva armonica. Nel sistema con numerosi gradi di libertà, queste oscillazioni sono descritti dal seguente sistema di equazioni differenziali lineari: dove M è una matrice quadrata simmetrica della massa; K è una matrice simmetrica di rigidezza piazza del sistema; F0 è un vettore di ampiezze di azione avvincente; ω è la frequenza di azione avvincente; u, u'' sono vettori di coordinate dei punti del sistema, che cambiano la loro posizione nel tempo t, e le loro accelerazioni; φ è la fase iniziale dell'eccitatore. |
| • | Forced oscillations of the system with the account of damping under action of harmonic compelling force. These oscillations are described by the following system of linear differential equations: |
| • | oscillazioni del sistema forzato al conto di smorzamento sotto l'azione del armonica forza avvincente. Queste oscillazioni sono descritti dal seguente sistema di equazioni differenziali lineari dove C è simmetrica matrice quadrata di smorzamento e u 'è vettore della velocità dei punti del sistema. Si assume che il sistema è smorzata conformemente al diritto Rayleigh, ossia è proporzionale alla distribuzione di rigidezze e le masse del sistema ed è definito con l'equazione dove a è un aspect ratio di masse e b è un rapporto di rigidità, entrambi i rapporti sono scalari. |
| • | oscillazioni forzate del sistema di entrambi i tipi di cui sopra, determinate dagli spostamenti dei supporti sotto la legge armonica, cioè portando uno o più sistema supporta allo spostamento oscillatorio. equazioni differenziali che descrivono questo tipo di oscillazioni sono analoghi a quelli stabiliti in precedenza, ma si differenziano per la forza armonica avvincente che viene calcolato tramite la formula: |
Diversi forze e/o spostamenti avvincenti possono essere applicate al sistema, ma le loro frequenze devono essere uguali.
La rotazione di un albero o mandrino nello stato sbilanciato su supporti elastici può servire un esempio di armonica forza attrattiva. eccitazione cinematica è applicata quando i valori delle forze convincenti non sono noti, a differenza di ampiezza delle oscillazioni di alcuni elementi strutturali che sono noti.
Quando si considera oscillazioni forzate, è importante prendere in considerazione l'impatto delle forze di smorzamento. Il processo di dissipazione di energia delle oscillazioni meccaniche, portando passo do po passo di attenuazione forfettarie prodotte da oscillazioni del sistema, viene definito "smorzamento". forze di smorzamento possono avere diversa origine, e cioè: l'attrito tra le superfici di scorrimento a secco, attrito tra superfici lubrificate, attrito interno, di aria o di resistenza del liquido, ecc Di solito presume che la forza di smorzamento è proporzionale alla velocità (smorzamento viscoso). forze di resistenza che cambiano in base alla legge volontaria vengono sostituiti per forze di smorzamento equivalenti, procedendo dalla condizione che in un ciclo, essi dissipano la stessa quantità di energia di forze reali. L'equazione per oscillazioni forzate con l'account di smorzamento per i-esimo di massa, che è la soluzione delle equazioni differenziali sopra, è il seguente:
![]() ,
,
dove ω0 è la frequenza angolare di smorzamento, ω è la frequenza angolare della forza attrattiva
2n=c/m ,
dove ci è fattore di smorzamento dell'i-esimo modo; e mi è la massa. Si compone di due termini: espressione in parentesi descrive attenuando oscillazioni libere a smorzamento frequenza che differisce di poco dalla frequenza delle oscillazioni libere; il resto corrisponde ad oscillazioni forzate con la frequenza d'azione forzata ω. Per chiarire l'impatto di smorzamento, consideriamo la figura che presenta il grafico della dipendenza del fattore di guadagno di ampiezze:
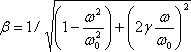
dal rapporto delle frequenze di oscillazioni forzate e libero ω/ω0 a diversi valori del fattore di smorzamento γ=n/ω=c/ccritico , dove ccritico è fattore critico di smorzamento viscoso, in cui oscillazioni non si verificano mentre lo spostamento del sistema decade monotonamente.

La figura mostra che, quando la frequenza delle oscillazioni forzate è basso rispetto alla propria frequenza delle oscillazioni libere, lo spostamento dei punti del sistema è approssimativamente uguale allo spostamento a carico statico, spinti dalla forza attrattiva. Quando la forza armonica guida ha alta frequenza, che indipendentemente dal fattore di smorzamento, non provocare oscillazioni forzate del sistema, che ha propria frequenza bassa. In entrambi i casi ω<<ω0 e ω>>ω0, smorzamento non crea impatto delle oscillazioni forzate, anche se quando il rapporto delle frequenze superiori è di circa 1, di smorzamento pone un impatto significativo sul fattore di guadagno. Al piccolo fattore di smorzamento, l'impatto maggiore di smorzamento si osserva nei pressi di frequenze di risonanza, che è fondamentale considerare quando si analizzano le strutture. Per scopi di analisi oscillazioni forzate di una struttura in prossimità proprie frequenze, importazione di valori di frequenze proprie dai risultati del calcolo della analisi in frequenza è fornito (vedere sotto).
Fattore di smorzamento γj per j th modo è legato a proporzioni a, b dall'equazione
![]() .
.
Il valore del fattore di smorzamento g assume valori da 0,01 per sistemi debolmente smorzate (parti tutti-metallo); 0,02-0,04 (strutture metalliche con giunti permanenti, che si deformano sotto il carico di snervamento); 0,03-0,07 (strutture metalliche con connessioni a taglio); 0,05 per la gomma; e fino a 0,15 per sistemi fortemente smorzate.
Se i fattori di smorzamento sono noti per la i th e il j th modo, di proporzioni saranno calcolati in formule:
![]() ,
,
![]() .
.
Se il coefficiente a è uguale a zero, tale smorzamento sarà chiamato relativo, e il fattore di smorzamento per j th modo sarà proporzionale alla frequenza angolare del modo senza smorzamento. Pertanto, oscillazioni corrispondenti ai modi superiori attenuano velocemente. Se il coefficiente b è uguale a zero, tale smorzamento verrà chiamato assoluta, e il fattore di smorzamento per j th modalità sarà inversamente proporzionale alla frequenza angolare di questa modalità senza smorzamento. Pertanto, le oscillazioni corrispondenti alle modalità più bassi saranno attenuano più lento.
I principali risultati del calcolo nel modulo di oscillazioni forzate sono i seguenti valori:
| • | ampiezze di spostamento a elementi finiti nodi mesh Um; |
| • | accelerazioni di vibrazione a elementi finiti nodi mesh espressi tramite ampiezze Um come U''m=Umω2 ; |
| • | sovraccarichi vibrazione, definito come il rapporto di vibrazione di accelerazione caduta libera U''m/g. |
Fasi dell'analisi delle oscillazioni forzate
| 1. | Creazione di uno “Studio”. Quando si crea uno studio, è necessario indicare il tipo, "Forced oscillazioni" nella finestra delle proprietà di comando. È possibile creare una copia di studio di tipo "analisi Frequency" e cambiare il tipo; in questo caso, le condizioni di maglia e di frontiera verrebbero trasferiti. |
| 2. | Impostazioni dei materiali. Per impostare i materiali, è necessario cliccare con il tasto destro del mouse sul corpo dalla cartella "Bodies" (o la cartella di per sé, al fine di impostare lo stesso materiale per tutti i corpi) e selezionare la voce "materiale". |
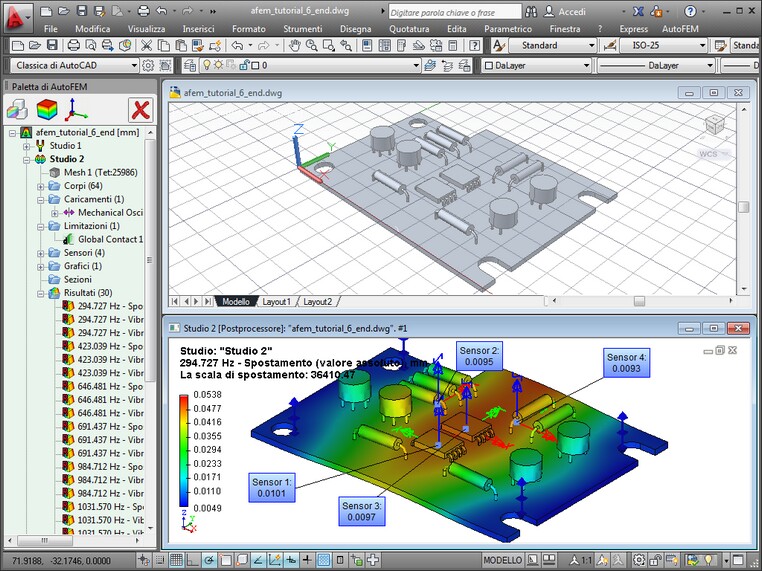
| 3. | Impostazioni delle condizioni al contorno. Nell'analisi di oscillazioni forzate, come nella analisi statica, fissaggio e carichi svolgono il ruolo di condizioni di confine. In questo tipo di analisi, tutti i tipi di fissaggi e carichi di forza possono essere utilizzati. Imporre gli elementi di fissaggio e di forza carichi è la condizione obbligatoria del calcolo essere corretta. In totale, i limiti imposti lo spostamento del corpo devono soddisfare la seguente condizione. Per l'analisi statica, il modello deve avere un fissaggio escluse sua muoversi liberamente nello spazio come il corpo solido. Il mancato rispetto di questa condizione porterebbe a risultati non corretti di modellazione agli elementi finiti o il fallimento del processo di calcolo. Inoltre, il carico cinematico "oscillatore" può sostituire fissaggi parziali o complete. |
| 4. | Impostazione frequenze e smorzamento ed esecuzioni dei calcoli. Prima del calcolo, l'utente deve indicare nelle proprietà dello studio i valori delle frequenze di azioni di carico, per il quale verrà effettuata l'analisi di oscillazioni forzate, nonché il valore di smorzamento. |
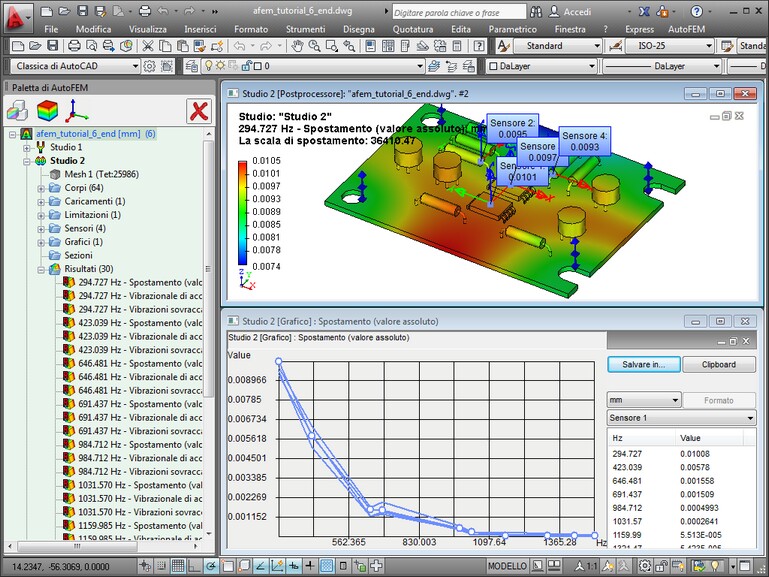
| 5. | Come ottenere ed analizzare i risultati. Per ottimizzare i risultati visualizzati, è necessario fare clic destro del mouse su cartella "Risultati" nell'albero di studi e selezionare la voce "Risultati". I risultati delle analisi delle oscillazioni forzate: ampiezze di spostamenti, di accelerazione di vibrazione per sovraccarichi di vibrazione, e fasi di oscillazioni. Per ogni tipo di risultato vi è l'opportunità di visualizzare lo stato deformato di una struttura in diverse fasi. |
Impostazioni specifiche del processo di pre-elaborazione nell'Analisi delle oscillazioni forzate
| 1. | Limitazione delle impostazioni. Il modello può essere limitato sia da limitazioni complete e parziali. Quando sono impostate limitazioni parziali, è vietato l'impostazione degli spostamenti diversi da zero. |
| 2. | Regolazione del carico della Forza. Per impostare l'ampiezza dei carichi forzati, i seguenti tipi di carichi possono essere applicati a facce, spigoli e vertici di un modello (accelerazione può essere applicato a organismi): |
| • | forza; |
| • | pressione; |
| • | accelerazione; |
| • | carico cilindrico |
| • | torsione. |
Un numero di carichi può dell'azione del sistema di corpi simultaneamente, ma tutti avranno la stessa frequenza. Per ciascuno dei carichi consentiti, proprio fase iniziale di oscillazioni può essere impostato.
| 3. | Regolazione del carico cinematica (oscillatore). Per impostare l'ampiezza di oscillazione del supporto, si deve applicare il carico oscillatore per elementi del modello, che può essere usato al posto di fissaggio completo o parziale. Il carico viene applicato sfaccettature, spigoli o vertici dei corpi, nonché organi singoli di concatenamento. Per specificare la direzione di oscillazioni LCS è selezionato nel comando, e la direzione stessa è indicato da un segno di spunta, corrispondente all'asse LCS rilevante. Il tipo di carico cinematica è scelto dal menu a tendina e potrebbe essere il seguente: |
| • | ampiezza del punto di spostamneto; |
| • | velocità; |
| • | accelerazione; |
| • | sovraccarico. |
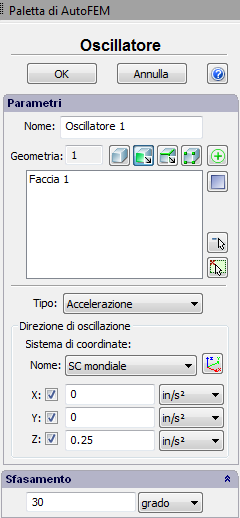
Nel campo separata, si può impostare lo sfasamento, misurata in gradi o radianti.
Alla combinazione di carico dell'oscillatore e fissaggi parziali, indicazioni di oscillazioni e limitazioni devono essere diversi per un singolo elemento del modello.
Impostazioni del processore di analisi oscillazioni forzate
In scheda [Generale], è possibile determinare o modificare le proprietà descrittive di questo studio; vale a dire: nome, tipo di studio, e commentare.
Nella scheda [Parametri], è possibile determinare o modificare le frequenze di azione esterna, i parametri di Rayleigh smorzamento.

Nel gruppo di parametri "Frequenze dell'azione esterna", sono stabiliti valori delle frequenze relative alle azioni di carichi esterni. Ci diversi modi di aggiungere nuovi valori:
| 1. | Bottone [Aggiungere] consente l'aggiunta sia del singolo valore della frequenza e una gamma di frequenza, per cui sono specificati il valore iniziale, valore finale e guadagno. |

| 2. | Bottone [Import] mette in evidenza la finestra di dialogo in cui i valori delle frequenze di risonanza possono essere importati fuori risultati delle analisi in frequenza eseguita in precedenza. |
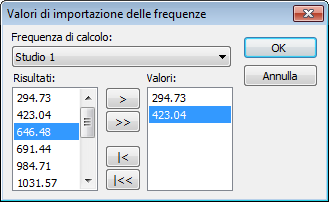
| 3. | Quando è necessario calcolare le oscillazioni forzate solo a tutte le frequenze di risonanza, determinati tramite l'analisi in frequenza in precedenza, è necessario attivare l'elemento di controllo "risultati dell'analisi Utilizzo frequenza". Qui, il collegamento associativo con i risultati dell'analisi frequenza selezionata viene mantenuta , cioè alla variazione dei risultati delle analisi di frequenza, i valori dei valori propri aggiornati saranno utilizzati automaticamente per l'analisi oscillazioni forzate. |
| 4. | Sopra la lista esistente di valori di frequenza, le seguenti operazioni di modifica sono disponibili: |
| • | bottone [Change] permette di ri-scrivere il valore del singolo valore specifico; |
| • | bottone [Rimuovi] rimuove il valore della frequenza selezionato dalla lista; |
| • | bottone [Clear] cancella fuori l'intero elenco di valori di frequenza. |
Nel gruppo di parametri "Rayleigh smorzamento", sono definiti i valori di smorzamento fattori della struttura a e b.
Tab [Risolvi] permette di impostare le proprietà del processore per la soluzione di un sistema di equazioni. Parametri, che definiscono le impostazioni del processore, sono simili a quelli della analisi statica.
La Tabella [risultati] permette di determinare i tipi di risultati, visualizzati nell'albero degli studi del calcolo.
Impostazione del processo di post-elaborazione dell'analisi dei risultati per le oscillazione forzate
Nella tabella [Risultati], si possono vedere i seguenti tipi di risultati suddivisi in otto gruppi:
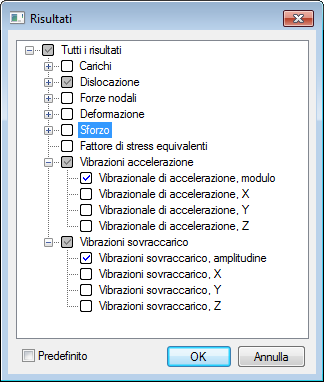
Il gruppo “Carichi” include i seguenti risultati: componenti applicati al modello elementi finiti e il modulo di carichi ridotti a nodi. Questo tipo di risultati sono per riferimento.
Il gruppo "spostamenti" comprende:
| • | Gli spostamenti dei punti del modello elementi finiti con il conto della fase di spostamento relativo alla fase di eccitatore nella direzione degli assi del sistema di coordinate globale (CS): |
| • | Parte reale di spostamenti in direzione degli assi di CS globale: Re(UX), Re(UY), Re(UZ), così come il modulo della parte reale degli spostamenti |
| • | Parte virtuale degli spostamenti in direzione degli assi di CS globale: Im(UX), Im(UY), Im(UZ), così come il modulo della parte visiva degli spostamenti |
| • | Ampiezza dello spostamento dei punti del modello elementi finiti (senza tener dello sfasamento relativo alla fase eccitatore) nella direzione degli assi di CS globale: UXm, UYm, UZm, così come il modulo di ampiezza |
| • | angoli di fase per componenti di spostamento dei punti del modello elementi finiti nella direzione degli assi di CS relative globale alla fase eccitatore |
Nel caso in cui lo sfasamento è preimpostato, si può separare la componente reale e virtuali degli spostamenti, così come il valore assoluto della fase nei punti del modello ad elementi finiti.
Nel gruppo "accelerazione di vibrazione", si può notare la derivazione di imperi di ampiezze di vibrazione accelerazioni relative ai punti del modello elementi finiti U''m=Umω2 ![]() . La fase di accelerazione di vibrazione differisce di 180 (π rad) dallo spostamento di fase.
. La fase di accelerazione di vibrazione differisce di 180 (π rad) dallo spostamento di fase.
Nel gruppo “Vibrazioni da sovraccarichi”, si può notare la derivazione degli imperi di sovraccarichi di vibrazione U''m/g, misurati in relazione dell'accelerazione caduta libera.
Inoltre è possibile visualizzare il grafico del risultato.