Strenth Theories. Appendix (references)

 

Properties of Structural Materials

A proper assignment of material properties used in the structure is an important prerequisite for correctness of finite element analysis. The main properties of structural materials used for strength analysis in AutoFEM are:

A material's Elastic Modulus E, [N/m2] - is the ratio of stress with respect to relative strain developing in a prism-shape speciment subjected to an axial force in a tensile test. In this case, a uniform stress state exists in the mid-part of the specimen in the longitudal direction. The value of the Elastic Modulus E on the strain graph is numerically equal to the tangent of the tilt angle of the linear segment: on the stress graph when testing a specimen. The physical sense of the E modulus is described as the stress required for doubling the specimen length. However, the value of elastic elongation seldom reaches even 1% for most of solid bodies.

The stress graph of the tested speciment has several special points corresponding to changes in physical properties of the material and is used for evaluating the degree of material reliability under load.

Elasticity limit σп - the stress that is the upper bound in effect of purely elastic strain.

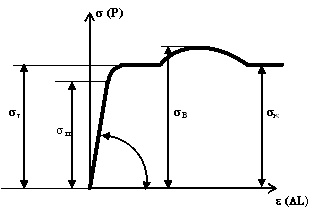
The stress (dilation) diagram for plastic materials (for example, low-carbon steel)

Yield limit σТ. Further elongation of the specimen (for example, for low-carbon steels) occurs practically with no increase in the load.This phenomenon is called "plastic flow", and the horizontal part of the diagram immediately to the right from the bend point is called the plastic flow range. In many structural materials the plastic flow range is not so prominently visible, as in low-carbon steels. The notion of the conditional yield limit σ s is introduced for such materials; this is the stress corresponding to the residual (plastic) strain equal to s %. Usually, s = 0.2%. The Yield Limit for plastic materials is selected as the strength criterion - the maximum safe stress [sy]. Reaching stresses corresponding to the yield limit causes irreversible plastic strains in the structure, thus breaking its viability and is thus an inadmissible behaviour from the safety viewpoint.

The ultimate strength sr (rheological resistance) is the stress, upon exceeding which the material rupture occurs. Upon an increase in the loads, there is a moment, after which more strain builds up in the specimen without an increase, or even under a reduction in, the load, up to the rupture.

The Poisson's ratio µ characterizes transverse strain developing in a stretching specimen. In the elastic zone, the strain in the transverse direction is , where ε - the strain in the longitudial direction, µ— the Poisson's ratio. For isotropical materials, the Poisson's ratio lies in the range .

For various steel grades, E = 195-206 GPa, µ = 0.23-0.31; for aluminum alloys, E = 69-71 GPa, µ = 0.30-0.33.

Elastic properties of some materials are given in the table (the denominator indicates the respective compression property).

A material's plasticity properties are the relative elongation and relative contraction at rupture:

,

where l0, F0 -the length of the working part of the specimen and the area of the cross-section before strain; lk - the length of the working part of the specimen after the rupture; Fk - the final area of the cross-section at the specimen's neck after the rupture.

The plastic and brittle material states are distinguished by the amount of relative elongation at rupture. Materials developing sufficiently high values at the point of rupture are referred to as plastic materials; those referred as brittle are the materials with relative elongation of . For plastic materials, upon compressing to nearly the yield condition, the graph pattern is the same as in the case of tension. Under a compression strain, the specimen shortens; meanwhile, its cross-section dimensions grow. For certain plastic materials, it is impossible to find the stress analogous to the tensile rheological resistance due to the specimen's flattening.

Brittle materials exhibit much better ability to resist compression strain, rather then dilational strain; for those, the compression rupture strain exceeds the ultimate tensile strength multifold. Rupture of brittle materials under compression occurs due to cracking.

 

Volume Stress-Strain State at a Point

The deformed state at a point of a deformable body is described by the symmetrical strain tensor:

,

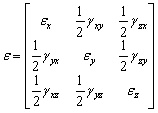where - the longitudinal relative strain, , , - the angular strain. You can always specify the three orthogonal directions, so that the sheer angles are all zeros, while elongations are . The strains , , in the directions, for which sheer angles are absent, are called principal strains at a point.

Together, the nine stress components (by three per each of the mutually perpendicular facets) make up a physical entity called, stress tensor at a point. The tensor is represented by a symmetrical matrix:

,

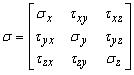where - the compression-tension stress, , ,, - the sheer stress.

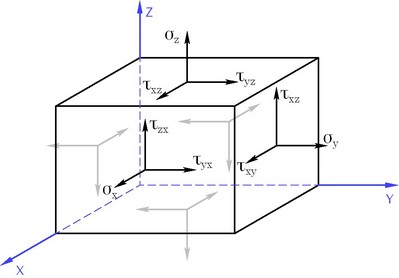
The stress state tensor components in an infinitesimal block

The following rule of signs is commonly used for stress tensor components: a component is positive, if it points in the positive direction of the respective coordinate axis of a facet with the positive external normal aligned with one of the coordinates.

Both the stress tensor and the strain tensor possess the symmetry property. , ,. The symmetry conditions of the stress tensor are also referred to as paired sheer stresses condition: the sheer stresses acting on two mutually perpendicular facets in the directions orthogonal to the edge in the intersection of those facets are equal in magnitude. Due to these properties, out of nine components of the stress tensor there are six independent ones.

Just like in the case of the strain, the concept of principal stresses is introduced in a stress state, , corresponding to principal strains, related with the stress tensor components by the equation:

, where

,       ,      

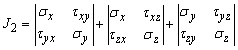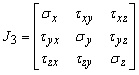
A cubic equation solution has three real roots , which are commonly ordered as follows: . The principal stresses possess an important property: the normal stresses on the principal direction-oriented facets are highest among those on any other facets. Also introduced is the concept of mean stress by the formula

 

Structure's Static Strength Assessment. Strength Theories

The ultimate safe stress state is when material properties undergo a qualitative change - a transition from one mechanical state to another one. For plastic materials, the safe strain state is commonly considered as the condition of developing noticeable residual strain, while for brittle ones - a condition when a material begins to crack. The ultimate state is not admissible for materials. Therefore, when performing strength analysis, pursue the so-called admissible state. It corresponds to the load obtained by dividing the load of the ultimate-strength state by a safety factor. If the safety factors are equal in two stressed states, than those are called equally fail-safe. To compare various strained states, the simple tension (compression) is accepted as the universal measure, with the principal stress .

Equivalent stress - the stress to be developed in a stretched specimen in order to make its state equally unsafe as a specified stress state. The strength criterion is written out as .

Strength theories are hypotheses about criteria describing the conditions of a material reaching the ultimate strength state.

 

First strength theory

In the first strength theory, a material's ultimate strength refers to the maximum normal stress. According to this theory, the unsafe state occurs when one of the principal stresses reaches a safety threshhold. Accordingly, the magnitude of the maximum principal stresses is limited so as not to exceed the maximum principal stress . The strength criterion appears as: , where , if and , if .

 

Second strength theory

The second strength theory uses the maximum strain as the ultimate strength criterion. According to this theory, the unsafe state of a material occurs when linear strain reaches a certain safety threshhold. For a plastic material, the strength criterion appears as , where . If, for example, , then .

For brittle materials, the strength criterion appears as:

,

The first theory yields good agreement with experimental data only for brittle materials. The second one is practically abandoned nowadays.

 

Third strength theory

In the third strength theory, the ultimate strength refers to the maximum sheer stress. According to this theory, the unsafe state occurs when the maximum sheer stress reaches a safety threshhold.

The strength criterion appears as: , where . Consequently:

 

Fourth (energy) strength theory

The fourth strength theory is based on the energy approach, based on the hypothesis that the cause of an unsafe state is the magnitude of the potential energy density of deformation uф, therefore the criterion refers to the density of the potential energy of deformation.

We will derive the formula for the potential energy density due to distortion from the formula for the full potential energy density due to strain, by using the specific Poisson's ratio of µ =0.5.

That yields:

The strength criterion appears as , where   .

Consequently:

or

The third and fourth strength theories produce satisfactory agreement of theoretical calculation results with laboratory test data for plastic materials and are widely used in strength analysis. These theories are not applicable for brittle materials.

 

Return to contents

autofem.com