Analysis of Rotating Solid Disc of Constant Thickness

Let us consider a disc of radius R and thickness h (see figure).

In analysis we consider only 1/4 th part of the disc with application of symmetry conditions at the corresponding edges (restraint of displacements in the direction of the axis of the local coordinate system perpendicular to the plane of the edge).
The disc is subjected to the centrifugal force F = ρω2R, where ρ - is the mass of the unit volume of the disc's material, ω - angular velocity of rotation.

Let us use the following data: radius of disc R is equal to 0.457, thickness of disc h is equal to 0.01 m, magnitude of angular velocity of rotation w is equal to 300 rad/s.
Material characteristics:E = 2.1E+011 Pa, ν  = 0.28, ρ = 7800 kg/m3 .
For this problem, displacements u can be determined from the formula:
,
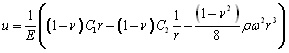where constants C1 = (3+ν)ρω2R2 / 8, C2 = 0 are determined from boundary conditions.
The displacement uR = (1-ν)ρω2R3/4E at r = R.

Stress components σr , σθ  are found as:

,

.
These stresses take the maximum value at the center of the disc where:
σr =σθ = (3+ν)ρω2R2 / 8

Thus, uR = 5.7430E-005 m, σr =σθ =σ = 6.0111E+007 Pa

After carrying out calculation with the help of AutoFEM, the following results are obtained:

Table 1.Parameters of finite element mesh

Table 2. Result "Displacement, magnitude"*

Table 3. Result "Equivalent Stress"*

 

Conclusions:

The relative error of the numerical solution compared to the analytical solution is equal to 0.21% for quadratic finite elements.

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the tables.

 

 

Read more about AutoFEM Static Analysis

autofem.com

Return to contents