Bar Subjected to Self-Weight

Let us consider a bar of radius R and length L, suspended at the upper edge and stretched under the action of self-weight (see figure).

Bar Subjected to Self-Weight, the finite element model with loads and restraints

The finite element model with applied loads and restraints

Let us use the following data: length of bar L is equal to 1 m, radius of cross-section of the bar R is equal to 0.02 m.
Material characteristics: E = 2.1E+011 Pa, ν = 0.28, ρ = 7800 kg/m3 .
Total elongation of the bar under the action of the self-weight can be determined from the formula:
ΔL = γL2/2E,
where γ – specific weight of the bar's material, that is γ = ρg, g ~ 9.80665 m/s2.
The stress in the cross-section of the bar located at a distance x from lower (unconstrained) edge can be evaluated from formula:
σ = γx
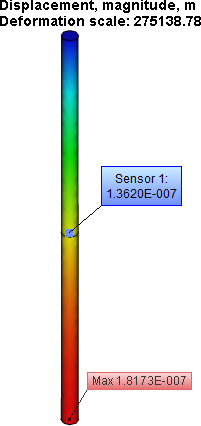
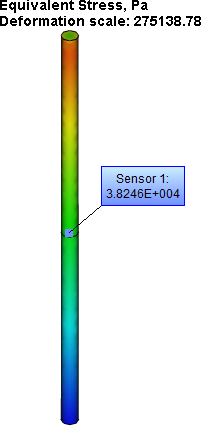
Thus, ΔL = 1.8212E-007 m; σ = 3.8246E+004 Pa at x = 0.5L.

After carrying out calculation with the help of AutoFEM, the following results are obtained:

Table 1.Parameters of finite element mesh

Finite Element Type	Number of nodes	Number of finite elements
quadratic tetrahedron	440	972

Table 2.Result "Displacement, magnitude"*

Numerical Solution Displacement w*, m	Analytical Solution Displacement w, m	Error δ = 100%* \|w* - w\| / \|w\|
1.8173E-007	1.8212E-007	0.21

Table 3. Result "Equivalent Stress"*

Numerical Solution Stress σ*, Pa	Analytical Solution Stress σ, Pa	Error δ = 100%* \|σ* - σ\| / \|σ\|
3.8246E+004	3.8246E+004	0.001

Bar Subjected to Self-Weight, the result "Dispacement, magnitude" of finite element modelling

Conclusions:

The relative error of the numerical solution compared to the analytical solution is 0.21% for displacements and 0,001% for stresses when using quadratic finite elements.

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the tables.