 |
 |
 |
 |
 |
 |
AutoFEM Analysis Große Auslenkung der kreisförmigen Platten unter einer gleichmäßig verteilten Last |  |
|
|
|
|
|
|
AutoFEM Analysis Große Auslenkung der kreisförmigen Platten unter einer gleichmäßig verteilten Last | |
Große Auslenkung der kreisförmigen Platten unter einer gleichmäßig verteilten Last
Betrachten wir einen kreisförmigen Platte mit dem Radius a und der Dicke h. Die Platte wird eingespannt und einer gleichmäßig verteilten Belastung mit der Intensität q (siehe Abbildung).
|
Die Finite-Elemente-Modell einer eingespannten kreisförmigen Platte unter einem gleichmäßig verteilter Last (große Auslenkung) |
Lassen Sie uns die folgenden ersten Daten: der Radius der Platte a beträgt 0.25 m, die Dicke der Platte h beträgt 0.005 m, die Belastungsintensität q ist 1E+05 Pa.
Materialeigenschaften sind: E=2.1E+011 and ν= 0.28.
Lassen Sie uns diese Näherungsformel Verschiebungen der Plattenmitte berechnen:
,
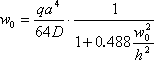wo
ist die Biegesteifigkeit der Platte.
Lösen dieser Gleichung für w0, so erhält man den Wert der maximalen Durchbiegung, die in der Mitte der Platte zu erwarten ist: w0= 2.3258E-003 m.
Nach Durchführung von Berechnungen (unter Berücksichtigung der Nichtlinearität) durch die AutoFEM Analyse folgende Ergebnisse erhalten:
Tabelle 1. Eigenschaften der Finite-Elemente-Netz
Art der Finite-Elemente |
Anzahl der Knoten |
Anzahl der finiten Elementen |
quadratische Tetraeder |
3000 |
8720 |
Tabelle 2.Ergebnis “Verschiebung, magnitude”
Numerische Lösung |
Analytische Lösung |
Fehler δ =100%*|w0*- w0|/| w0 | |
2.2938E-003 |
2.3258E-003 |
1.38 |
|
*Die Ergebnisse der numerischen Berechnungen hängen von der Finite-Elemente-Netz und können leicht abweichen von den in den Tabellen angegeben.
Lesen Sie mehr über AutoFEM Static Analysis
