Spannungen und Verformungen eines orthotropen Platte bei biaxialen Spannung

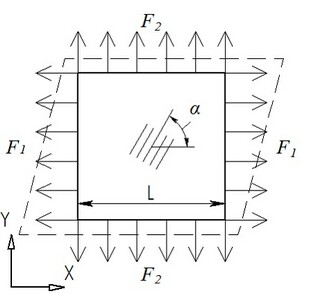
Betrachten wir eine quadratische Platte des orthotropen Material hergestellt, wobei die Länge L der Seitenwand, die mit den Kräften F1 und F2, die an Kanten der Platte geladen wird. Die Breite der Platte ist h.
Wir müssen Spannungen und Verformungen der Platte zu definieren. Angenommen  F1=20,000 N, F2=10,000 N, L=0.1 m, und h=0.005 m.
Parameter des Materials sind wie folgt: Module der Elastizität sind Е1=5.59·1010 Pa, Е2=1.373·1010 Pa, Е3=1.373·1010 Pa, Module von Scherung sind G12=5.59·109 Pa,  G23=4.904·109 Pa,  G31=5.59·109 Pa, und Poisson-Koeffizienten sind ν12=0.277, ν23=0.4, ν31=0.068. Der Elevationswinkel des Haupt Symmetrieachse α=45°.

In der Mitte der Platte, schaffen wir eine Benutzer-Koordinatensystem (namens "Ortho") mit AutoCAD-Befehl "UCS" und importieren Sie dann in AutoFEM Analysis.
Dieses Koordinatensystem definieren die Anisotropieachsen des Materials der Platte. Um sie zu setzen, sollten wir über das Kontextmenü-Befehl "Anisotropy Eigenschaften".

Um das Modell zu stabilisieren, aktivieren Sie das Kontrollkästchen "Stabilisieren Sie den fixierten Modell" (Seite "Lösen" der Studie Eigenschaften).
Apply normal load with magnitude  to one pair of parallel lateral facets, and normal load F2, to another pair.

Anwenden Normallast mit Größenordnung F1 einem Paar von parallelen seitlichen Facetten und normaler Last F2, um ein anderes Paar.

Lassen Sie uns durch eine statische Berechnung für die Platte mit der Verwendung des Befehls "Berechnung".

Wir erhalten Ergebnisse in Form von Verformungen und Spannungen.

 

 

Durchschnittlicher Wert der Verformung ОХ εx*=3.177·10-4, der Verformung ОY εy*=2.107·10-3,

Haupt-Spannungen sind: σ1*=4,000·107 Pa, σ2*=2,000·107 Pa.

Die analytische Lösung für die wichtigsten Spannungen hat die folgende Form:

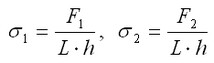
σ1=20000/0.005/0.01=4·107 Pa, σ2=10000/0.005/0.01=2·107 Pa.

Verformungen entlang der Achsen OX, OY werden unter Verwendung der folgenden Formel:

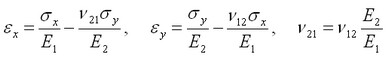
ν21=0.277·1.373·1010/5.59·1010=0.06804
εx=3.0·107/5.59·1010 – 0.06804·3.0·107/1.373·1010=3.88·10-4;
εy=3.0·107/1.373·1010 – 0.277·3.0·107/5.59·1010=2.036·10-3;

Nach Berechnungen mit Hilfe der AutoFEM Analyse nach der direkten Methode durchgeführt wurden, haben wir die folgenden Ergebnisse erzielt:

Tabelle 1.

Tabelle 2.

Tabelle 3.

 

 

*Die Ergebnisse der numerischen Untersuchungen hängen von der Finite-Elemente-Netz und können geringfügig von den in der Tabelle angegeben.

 

Lesen Sie mehr über  AutoFEM Static Analysis

Zurück zum Inhaltsverzeichnis