El contacto entre una barra cilíndrica y un anillo

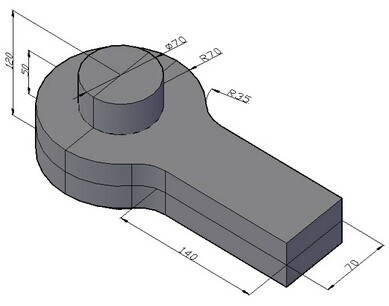
Consideremos el contacto entre la barra cilíndrica y el anillo (ver figura). Se supone que las partes no están atados juntos
Cada parte puede se mueve libremente por el otro (sin fricción).

La fuerza normal P se aplica a los extremos libres del anillo. La magnitud de la fuerza es 1E 005 N.

Usemos los siguientes datos iniciales: el diámetro del eje cilíndrico d is 0.07 m, la longitud del eje H is 0.12 m,

el radio exterior del anillo de ojo R es 0.07 m, el espesor h del anillo ocular es 0.05 m, la anchura de la cinta del anillo de ojo b es 0.07 m, la longitud de la cinta del anillo de ojo L es 0.14 m, el radio de transición del anillo del ojo r es 0.035 m.
Propiedades de los material en el módulo de elasticidad E = 2.1E+011 Pa y El coeficiente de Poisson ν = 0.28.
La tensión normal en la sección de la correa se puede calcular utilizando la siguiente fórmula semiempírica:

σ = k*P / h*(2*R - d)

Donde P es la fuerza normal, k es el factor de concentración de tensión (k = 3,6).

El cálculo utilizando las fórmulas anteriormente mencionadas da el resultado: σ = 1.0286E+008 Pa.
Después de la realización de los cálculos por el Análisis AutoFEM se obtiene el siguiente resultados : los rangos normales Tensión σX rangos de 0.8E+008 Pa a 0.99E+008 Pa. Vamos a comparar σX con σ:

Tabla 1. Parámetros de la malla de elementos finitos

Tabla 2.The resultado “Normal Tensión OX”*

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

 

Lea más acerca de AutoFEM Static Analysis

autofem.com

Volver al índice