Fuente de calor distribuida aplicada a la superficie cilíndrica interior del disco

Vamos a considerar un problema de distribución en estado estacionario de la temperatura en la cara final del disco dentro de la cual hay un calentador en forma de una superficie cilíndrica con un radio rd=20 mm, poder P=100 W,y en la periferia una temperatura constante de 273.15 oK se lleva a cabo.

Parámetros de un disco: disco de metal de espesor d=5 mm, radio  R=100 mm y conductividad térmica K=50 W/(m • oK) – Térmico conductividad de un disco en el interior fuera de la superficie cilíndrica del calentador es el mismo. [aleación de acero (SS)]. (ver la figura).

 

La solución de este problema, en la que se considera como la fuente distribuida, puede obtenerse resolviendo el problema de una fuente puntual de calor (como en el ejemplo anterior). Sea el origen coincide con un centro de una superficie circular de un disco. El es que ecuación diferencial que hay que resolver para una fuente puntual tiene la forma:

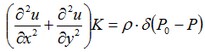
Donde ρ densidad de potencia distribuida. Se conoce la solución de esta ecuación. Para nuestro case: ρ = P/ (2π•rd•d) = P/S, Donde S –  área de la superficie del cilindro. Al tomar en cuenta la distribución del poder en todo el anillo del cilindro, expresamos la temperatura como una potencia total de todas las fuentes puntuales aplicadas por la integración de la función delta, en el lado de la derecha, sobre el punto de P0 . Como resultado, se obtiene una ecuación:

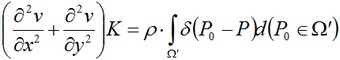
Donde Ω – es un conjunto de puntos de la superficie de un disco, Ω "- es un conjunto de puntos que se encuentran dentro de la superficie de un disco y delimitadas por un anillo de un cilindro sobre el que se prescribe el poder. La solución de este ν ecuación es una combinación lineal (integrante) de soluciones para fuentes puntuales:

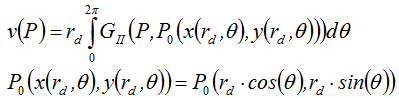
Donde GII – Es una función de Green para una potencia definida por la fórmula ρ = P/S, para su distribución en la superficie. Después de la integración, se obtiene:

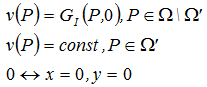
Donde GI –es una función de Green para una potencia definida por la fórmula  ρ = P/S para una fuente puntual distribuida en el borde. Esto implica que la magnitud de la ν temperatura coincidirá con la temperatura de una fuente puntual (situado en el centro de un círculo) para los puntos que se encuentran fuera con respecto al anillo en la que se prescribe la fuente de calor distribuida. En los puntos internos, la Temperatura tomará el valor igual a una constante. Tenga en cuenta que ν – es una función continua y esto es por qué el valor de la constante en el interior del cilindro incrustado siempre se conoce.

Comparemos solución analítica con la solución obtenida a partir de AutoFEM. Después de llevar a cabo el cálculo de los siguientes resultados se obtienen:

Tabla 1. Parámetros de malla de elementos finitos

Tabla 2. Resultado " temperatura "

 

Compare esta parcela con un campo generado por la fuente distribuida a lo largo del borde. Vemos que coinciden.

Conclusiones:

Para un problema determinado se obtuvo una imagen realista del campo temperatura. El error relativo de la solución numérica. en comparación con la analítica solución no exceder de 0,08% cuando se usa elemento lineal en el borde de un disco.

Además, observamos que el modelado de un problema con la fuente distribuida por una fuente puntual era muy posible. No pretendemos que siempre es posible. Sin embargo, para ciertas geometrías esto se puede hacer. Por ejemplo, en nuestro caso, la fuente de calor distribuida tenía una simetría central.

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

Lea más acerca de AutoFEM Térmico Analysis

autofem.com

Volver al índice