Gran deflexión de una placa circular bajo una carga uniformemente distribuida

Consideremos una placa circular con el radio a y el espesor h. La placa se sujeta y sometida a una carga distribuida de manera uniforme con la intensidad Q (ver la Figura).

Vamos a usar los siguientes datos inicial: el radio de la placa a es 0,25 m, el espesor de la placa de h es 0,005 m, la intensidad de la carga q es 1E 05 Pa.

Propiedades de los materiales son E = 2.1E 011 yn = 0,28.

Vamos a usar la siguiente fórmula aproximada para calcular desplazamientos del centro de la placa:
,
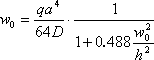Donde:

es la rigidez a la flexión de la placa.

Resolviendo esta ecuación para w0, se obtiene el valor de la deflexión máxima, que se espera en el centro de la placa: w0= 2.3258E-003 m.

Después de la realización de los cálculos (teniendo en cuenta la no linealidad) por el análisis AutoFEM se obtienen los siguientes resultados (número de fases de carga es de 6):

Tabla 1. Parámetros de la malla de elementos finitos

Tabla 2. El resultado "Desplazamiento, magnitud"

Conclusiones:

El error relativo de la solución numérica. en comparación con la solución analítica de es Igual a 0,92% para los elementos finitos cuadráticas.

 

* Las pruebas de los resultados numericos dependen del elemento finito meshymay difieren ligeramente de los que figuran en las tablas.

 

Lea más acerca de AutoFEM Static Analysis

autofem.com

Volver al índice