 |
 |
 |
 |
 |
 |
AutoFEM Analysis Tensiones y deformaciones de una placa ortotrópica en biaxial tensión |  |
|
|
|
|
|
|
AutoFEM Analysis Tensiones y deformaciones de una placa ortotrópica en biaxial tensión | |
Tensiones y deformaciones de una placa ortotrópica en biaxial tensión
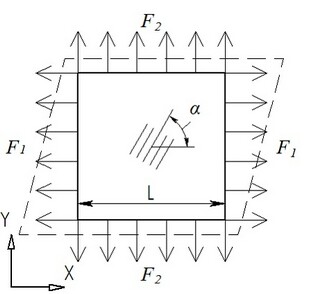
Consideremos una placa cuadrada hecha de material ortotrópico, con la longitud de la banda L, que se carga con las fuerzas F1 y F2, aplicado a los bordes de la placa. La anchura de la placa es h.
Tenemos que definir Tensiones y deformaciones de la placa. asumir F1=20,000 N, F2=10,000 N, L=0.1 m,yh=0.005 m.
Los parámetros de los materiales son los siguientes: Módulo de elasticidad son Е1=5.59·1010 Pa, Е2=1.373·1010 Pa, Е3=1.373·1010 Pa, módulos de cizallamiento son G12=5.59·109 Pa, G23=4.904·109 Pa, G31=5.59·109 Pa, y los coeficientes de Poisson están ν12=0.277, ν23=0.4, ν31=0.068. El ángulo de elevación del eje principal de simetría es α=45°.
En el centro de la placa, vamos a crear un usuario del sistema (llamado "Ortotrópico") coordinar el uso de AutoCAD comando "UCS" y luego importarlo a AutoFEM Análisis.
Este sistema de coordenadas se definen los ejes de anisotropía del material de nuestra placa. Para establecerlas, debemos utilizar el contexto del mandato "propiedades" de anisotropía.
Para estabilizar el modelo, marca la casilla "estabilizar el modelo no fijado" (página "Resuelve" de las propiedades del estudio).
Aplique la carga normal con magnitud F1 para un par de facetas laterales paralelos y F2 carga normal, a otro par.
|
El modelo de elementos finitos de la placa ortotrópica con cargas y sujeciones. |
Realicemos un cálculo estático para la placa con el uso del comando "Cálculo".
Vamos a obtener resultados en forma de deformaciones y tensiones.
|
Principio 1 Tensión de la placa ortotrópica |
|
Principio 2 Tensión de la placa ortotrópica |
Valor medio de la deformación ОХ εx*=3.177·10-4,de deformación ОY εy*=2.107·10-3,
Tensiones principales son: σ1*=4,000·107 Pa, σ2*=2,000·107 Pa.
La Solución Analítica para principales Tensiones toma la siguiente forma:
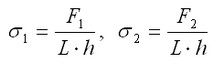
Donde F1,2 significa fuerza N, L significa la longitud de la placa, y h significa anchura de la placa, m.
σ1=20000/0.005/0.01=4·107 Pa, σ2=10000/0.005/0.01=2·107 Pa.
Las deformaciones a lo largo de los ejes OX, OY
se calculan utilizando las siguientes fórmulas:
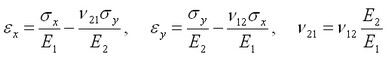
ν21=0.277·1.373·1010/5.59·1010=0.06804
εx=3.0·107/5.59·1010 – 0.06804·3.0·107/1.373·1010=3.88·10-4;
εy=3.0·107/1.373·1010 – 0.277·3.0·107/5.59·1010=2.036·10-3;
Después de los cálculos realizados con la ayuda de AutoFEM Análisis por el método directo, se han obtenido los siguientes resultados:
Tabla 1
Tipo de elemento finito |
Número de nodos de esquina |
Número de elementos finitos. |
tetraedro cuadrática |
2056 |
6897 |
Tabla 2
Principal Tensión |
Resultado numérico, σ* |
Resultado Analítico, σ |
Error, |
σ1 ,Pa |
4.0x107 |
4.0x107 |
0.00% |
σ2 ,Pa |
2.0x107 |
2.0x107 |
0.00% |
Table 3
Cepas |
Resultado numérico, σ* |
Resultado Analítico, σ |
Error, |
ε OX |
3.177x10-4 |
3.88x10-4 |
18.11% |
ε OY |
2.107x10-3 |
2.036x10-3 |
3.48% |
Conclusiones:
El error relativo de la solución numérica. en comparación con la solución analítica es <1E-005% para los Desplazamientos y 18,11% para las cepas utilizando elementos finitos cuadráticas.
Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.
Lea más acerca de AutoFEM Static Analysis
