 |
AutoFEM Analysis Las vibraciones de una placa simplemente apoyada debido al punto medio de oscilación | ||||||
 |
AutoFEM Analysis Las vibraciones de una placa simplemente apoyada debido al punto medio de oscilación | ||||||
Las vibraciones de una placa simplemente apoyada debido al punto medio de oscilación
Consideremos una placa simplemente apoyada, la sección central de los cuales oscila armónicamente con una amplitud de 0,5 mm. (ver la Figura)
|
Nuestro objetivo es encontrar amplitudes de oscilación de un punto con coordenadas x utilizando las frecuencias especificadas.
Usemos los siguientes datos iniciales: longitud de la placa L = 850 mm, la sección transversal es un rectángulo con ancho b = 75 mm, altura h = 5 mm. Fuerza armónica se aplica en un punto con x = 0,5 L = 212,5 mm.
Parámetros del material: módulo de elasticidad E=2.1E+011Pa, el coeficiente de Poisson ν=0.28, densidad γ=7800kg/m3.
Solución analítica clásica
(Resonantes) las frecuencias propias del sistema son:

Donde Jx=bh3/12 - el momento de inercia de la sección transversal;
f1,2,3,4= 16.2826; 65.1304; 146.5434; 260.5216. Así, primero Frecuencia naturales cae en el rango 4Hz to 32Hz.
Deflexión dinámica en el punto x se calcula mediante la fórmula:
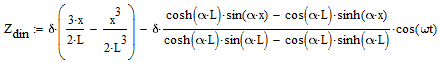
![]() .
.
La deformación máxima se alcanza en peso = p. Deflexión bajo la carga dinámica en 4Hz to 32Hz: ΔZdyn = 0.344039; 0.344910; 0.346381; 0.348479; 0.351244; 0.354734; 0.359022; 0.364205 mm.
Solución numérica.
Vamos a resolver este estudio por paquete AutoFEM Análisis. Ambos extremos son restringidos para simular el apoyo simple: Desplazamientos del extremo izquierdo en el eje X y el eje Z están prohibidas y sólo rotación alrededor del eje y se permite; Desplazamientos del extremo derecha a lo largo y eje Z están prohibidas y sólo rotación alrededor y - se permite eje.
|
El modelo de elementos finitos con cargas y restricciones aplicadas |
Las primeras frecuencias propias es igual to f(1)n =16.286 Hz (el modo de resultado " 01 (16.286 Hz)" del estudio ("estudio 2 (frecuencias propias)").
Amplitudes de vibración tienen los siguientes valores: Z*dyn= ver tabla 2 (Resultados"4.000 Hz-Forma, amplitud Z ... 32.000 Hz-Forma, Amplitud Z "del estudio" Estudio 3 (oscilaciones forzadas)").
Vamos a comparar los resultados de cálculo:
Tabla 1. Parámetros de la malla de elementos finitos
Tipo de elementos finitos. |
Número de Nodos |
Número de elementos finitos. |
triángulo lineal |
585 |
256 |
Tabla 2. Los Resultados
Frecuencia ff , Hz |
Solución analítica |
Solución numérica. |
Error δ = 100* | R* - R | / | R |, % |
4 |
0.344039 |
0.3462 |
0.63 |
8 |
0.344910 |
0.3479 |
0.87 |
12 |
0.346381 |
0.3508 |
1.28 |
16 |
0.348479 |
0.3549 |
1.84 |
20 |
0.351244 |
0.3604 |
2.61 |
24 |
0.354734 |
0.3672 |
3.51 |
28 |
0.359022 |
0.3757 |
4.65 |
32 |
0.364205 |
0.3859 |
5.96 |

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.
Lea más acerca de Análisis AutoFEM Oscilaciones