Forced Oscillation of a Simply Supported Plate

Let us consider a simply supported plate loaded with harmonic force (see figure).

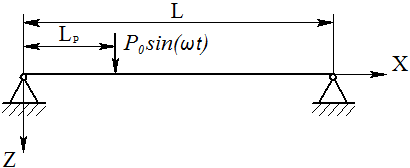
The force applied at distance c varies with time by harmonic law:

P(t)=P0sin(ωft),

where  P0 is equal to 125 N.

ωf= 2π ff ,

where the frequency ff ranges from 4Hz to 32Hz.

Our aim is to find oscillation amplitudes of a point with coordinate x using the specified frequencies.

Let us use the following initial data: length of the plate L = 850 mm, the cross section is a rectangle with width b = 75 mm, height h = 5 mm. Harmonic force is applied at a point with x=Lp=0.5L=425 mm.

Parameters of the material: modulus of elasticity E=2.1E+011Pa, Poisson's ratio ν=0.28, density γ=7800kg/m3.

Classic analytical solving

Natural (resonant) frequencies of the system are:

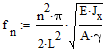
f1,2,3,4= 16.2826; 65.1304; 146.5434; 260.5216. Thus, first natural frequency falls in range 4Hz to 32Hz.

Static deflection at point x is calculated by formula (retaining 15 terms in a sum):

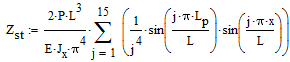
Where Jx=bh3/12 - the moment of inertia of cross-section.

Thus, deformation under the static load ΔZst = 9.747628 mm.

Dynamic deflection at point x is calculated by formula (retaining 15 terms in a sum):

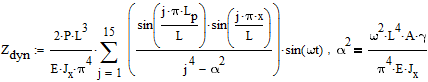
Maximum deformation is attained at ωt=π/2. Deflection under the dynamic load at 4Hz to 32Hz:  ΔZdyn = 10.364731; 12.805064; 21.169956; 279.32888; -18.741249; -8.049125; -4.763555; -3.20966 mm.

Numerical solution

Let us solve this study by AutoFEM Analysis package. Both ends are restrained to simulate simple support: displacements of the left end along XYZ-axis are forbidden and rotation only around Y-axis is allowed; displacements of the right end along YZ-axis are forbidden and rotation only around Y-axis is allowed.

The static displacement of the system is ΔZ*st = 9.7570 mm (the result "Displacement OZ" of the study "Study 1 (Static Analysis)").

First eigenfrequency is equal to f(1)n =16.291 Hz (the result "Mode 01 (16.291 Hz)" of the study "Study 2 (Frequency Analysis)").

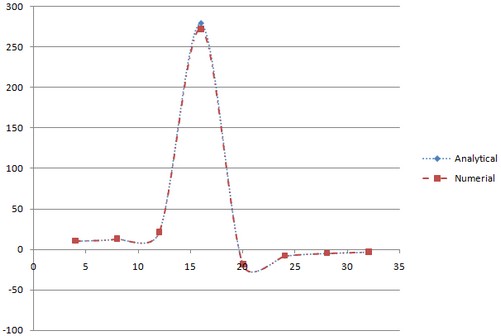
Vibrational amplitudes have the following values: Z*dyn= see table 2 (results "4.000 Hz Displacement OZ ... 32.000 Hz Displacement OZ" of the study "Study 3  (Forced Oscillations)").

Let us compare the results of calculation:

Table 1. Parameters of the finite element mesh

Table 2. The results

 

 

 

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.

** The negative signs are applied inversely, because Z-axis of results is directed up.

 

Read more about AutoFEM Oscillations Analysis

autofem.com

Return to contents