 |
 |
 |
 |
 |
 |
AutoFEM Analysis Oscillazione forzata di una piastra semplicemente appoggiata |  |
|
|
|
|
|
|
AutoFEM Analysis Oscillazione forzata di una piastra semplicemente appoggiata | |
Oscillazione forzata di una piastra semplicemente appoggiata
Consideriamo una piastra semplicemente appoggiata caricato con forza armonica (vedi figura).
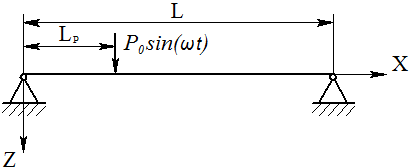
La forza applicata alla distanza k varia nel tempo dalla legge armonica:
P(t)=P0sin(ωft),
dove P0 è uguale a 125 N.
ωf= 2π ff ,
dove la frequenza ff ha un intervallo che varia da 4Hz a 32Hz.
Il nostro obiettivo è quello di trovare ampiezze di oscillazione di un punto con coordinate x utilizzando le frequenze specificate.
Usiamo i seguenti dati iniziali: lunghezza della piastra L = 850 mm, la sezione trasversale è un rettangolo con larghezza b = 75 mm, altezza h = 5 mm. Forza armonica viene applicata in un punto di x = Lp = 0.5L = 425 millimetri.
Parametri del materiale: modulo di elasticità E = 2.1E + 011 Pa, coefficiente di Poisson ν=0.28, densità γ=7800kg/m3.
Risoluzione Analitica Calssica
Naturali (risonanti) frequenze del sistema sono:
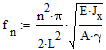
f1,2,3,4= 16.2826; 65.1304; 146.5434; 260.5216. Perciò, prima frequenza naturale cade nell'intervallo da 4Hz a 32Hz.
Deflessione statica al punto x viene calcolato dalla formula (15 mantenendo in termini di una somma):
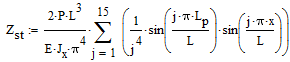
Dove Jx=bh3/12 - momento di inerzia della sezione trasversale.
Perciò, deformazione sotto carico statico ΔZst = 9.747628 mm.
Deflessione Dinamica a punto x viene calcolato dalla formula (15 mantenendo in termini di una somma):
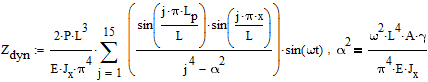
Deformazione massima viene raggiunta wt = p / 2. Flessione sotto il carico dinamico a 4 Hz a 32Hz: ΔZdyn = 10,364731; 12.805064; 21.169956; 279,32888; -18,741249; -8,049125; -4,763555; -3.20966 Mm.
Numerica Soluzione
Cerchiamo di risolvere questo studio pacchetto di AutoFEM Analysis. Entrambe le estremità sono trattenuti per simulare supporto semplice: spostamenti del fine sinistra lungo XYZ sono proibiti e la rotazione solo circa asse Y è consentito; spostamenti del fine destra lungo YZ asse sono proibiti e la rotazione soltanto intorno all'asse Y è permesso.
|
Il modello ad elementi finiti con carichi applicati e vincoli |
Lo spostamento statico del sistema è Az * v = 9,7704 mm (il risultato "Displacement OZ" dello studio "Study 1 (flessione statica)").
Prima eigenfrequency è pari a f (1) n = 16,286 Hz (il risultato "Modo 01 (16,286 Hz)" dello studio "Studio 2 (frequenze proprie)").
Ampiezze vibrazionali hanno i seguenti valori: Z Din = vedi tabella 2 (risultati "4.000 Hz Displacement OZ ... 32.000 Hz Spostamento OZ" dello studio "Studio 3 (oscillazioni forzate)").
Mettiamo a confronto i risultati di calcolo:
Tabella 1. Parametri della mesh ad elementi finiti
Tipo di Elemento Finito |
Numero di Nodi |
Numero di Elementi Finiti |
linear triangle |
585 |
256 |
Tabella 2. I resultati
Frequenza ff , Hz |
Soluzione Analitica |
Soluzione Numerica |
Errore δ = 100* | R* - R | / | R |, % |
0 |
9.747628 |
9.7704 |
0.23 |
4 |
10.364731 |
10.3747 |
0.10 |
8 |
12.805064 |
12.8143 |
0.07 |
12 |
21.169956 |
21.1684 |
0.01 |
16 |
279.32888 |
272.9463 |
2.28 |
20 |
-18.741249 |
-18.8049 |
0.34 |
24 |
-8.049125 |
-8.0679 |
0.23 |
28 |
-4.763555 |
-4.7727 |
0.19 |
32 |
-3.20966 |
-3.2150*2 |
0.17 |
|
* I risultati dei test numerici dipendono elementi finiti maglia e possono differire leggermente da quelli indicati nella tabella.
** I segni negativi sono applicati inversamente, perché l'asse Z dei risultati è diretto in su.
RApprofondire riguardo ad AutoFEM Oscillations Analysis
