 |
AutoFEM Analysis Vibrazioni di una piastra supportata ia bordi a casua delle oscillazioni nel punto medio | ||||||
 |
AutoFEM Analysis Vibrazioni di una piastra supportata ia bordi a casua delle oscillazioni nel punto medio | ||||||
Vibrazioni di una piastra supportatata ai bordi a causa delle oscillazioni nel punto medio
Consideriamo una piastra semplicemente appoggiata, la sezione centrale di che oscilla armonicamente con un'ampiezza di 0,5 mm. (vedi figura)
|
Il nostro obiettivo è quello di trovare ampiezze di oscillazione di un punto con coordinate x utilizzando le frequenze specificate.
Usiamo i seguenti dati iniziali: lunghezza della piastra L = 850 mm, la sezione trasversale è un rettangolo con larghezza b = 75 mm, altezza h = 5 mm. Forza armonica viene applicata in un punto di x = 0,5 L = 212,5 millimetri.
Parametri del materiale: modulo di elasticità E = 2.1E + 011 Pa, coefficiente di Poisson ν=0.28, densità γ=7800kg/m3.
Classica Soluzione Analitica
Naturali (risonanti) frequenze del sistema sono:
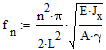
Dove Jx=bh3/12 - momento di inerzia della sezione trasversale;
f1,2,3,4= 16.2826; 65.1304; 146.5434; 260.5216. Perciò, prima frequenza naturale rientra nell'intervallo compreso tra 4 Hz e 32Hz.
Deflessione Dinamica a punto x viene calcolato dalla formula:
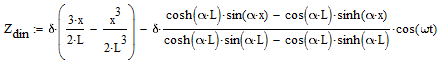
![]() .
.
Deformazione massima viene raggiunta wt = p. Flessione sotto il carico dinamico a 4 Hz a 32Hz: ΔZdyn = 0,344039; 0.344910; 0.346381; 0.348479; 0.351244; 0.354734; 0.359022; 0.364205 mm.
Soluzione numerica
Cerchiamo di risolvere questo studio pacchetto di AutoFEM Analysis. Entrambe le estremità sono trattenuti per simulare supporto semplice: spostamenti del fine sinistra lungo XYZ sono proibiti e la rotazione solo circa asse Y è consentito; spostamenti del fine destra lungo YZ asse sono proibiti e la rotazione soltanto intorno all'asse Y è permesso.
|
Il modello ad elementi finiti con carichi applicati e vincoli |
Prima eigenfrequency è pari a f (1) n = 16,286 Hz (il risultato "Modo 01 (16,286 Hz)" dello studio "Studio 2 (frequenze proprie)").
Ampiezze vibrazionali hanno i seguenti valori: Z * din = vedi tabella 2 (risultati "4.000 Hz-Form, Ampiezza Z ... 32.000 Hz-Form, Ampiezza Z" dello studio "Studio 3 (oscillazioni forzate)").
Mettiamo a confronto i risultati di calcolo:
Tabella 1. Parametri della mesh ad elementi finiti
tipo di Elemento Finito |
Numro di nodi |
Numero di Elementi Finiti |
triangolo lineare |
585 |
256 |
Tabella 2. I Risultati
Frequenza ff , Hz |
Soluzione Analitica |
Soluzione Numerica |
Errore δ = 100* | R* - R | / | R |, % |
4 |
0.344039 |
0.3462 |
0.63 |
8 |
0.344910 |
0.3479 |
0.87 |
12 |
0.346381 |
0.3508 |
1.28 |
16 |
0.348479 |
0.3549 |
1.84 |
20 |
0.351244 |
0.3604 |
2.61 |
24 |
0.354734 |
0.3672 |
3.51 |
28 |
0.359022 |
0.3757 |
4.65 |
32 |
0.364205 |
0.3859 |
5.96 |

* I risultati dei test numerici dipendono elementi finiti maglia e possono differire leggermente da quelli indicati nella tabella.
Approfondire riguardo ad AutoFEM Oscillations Analysis