 |
 |
 |
 |
 |
 |
AutoFEM Analysis Campo di temperatura non in regime stazionario in una piastra ortropa |  |
|
|
|
|
|
|
AutoFEM Analysis Campo di temperatura non in regime stazionario in una piastra ortropa | |
Campo di temperatura non in regime stazionario in una piastra ortotropa
Confrontiamo un problema bidimensionale di raffreddamento della grafite con proprietà ortotropiche. La temperatura iniziale della piastra è t0=60 °С. La temperatura sui bordi della piastra è mantenuta uguale a zero. La piastra si raffredda in un periodo di 20 secondi. Si determini il campo di temperatura al tempo t1-4 = 2, 5, 10 sec. Il calcolo del campo di temperatura sarà condotto sui punti di controllo da 1-5 con coordinate (Xi,Yi):
i |
1 |
2 |
3 |
4 |
5 |
X, mm |
20 |
20 |
80 |
80 |
50 |
Y, mm |
20 |
80 |
20 |
80 |
50 |
|
Il sistema di coordinate è stato scelto in modo che l'origine del sistema di coordinate coincide con l'angolo del piatto, e la direzione lungo la base è la direzione selezionata lungo l'asse OY.
LE proprietà della piastra ortotropica: densità ρ=2.5 g/cm3, calore specifico c=840 J/(kg •°K), coefficiente della conduttività termica: K1=0.139 W/(mm •°K) (lungo l'asse OX); K2=0.278 W/(mm • °K) (lungo l'asse OY – direzione della base). La piastra ha una forma rettangolare 100 × 100 mm.
L'equazione differenziale ha forma:
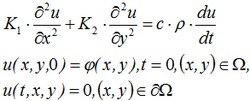
where ∂Ω – the boundary of the numerical domain. Analytical solution of the problem has the form2*:
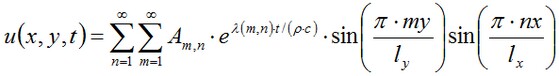
where
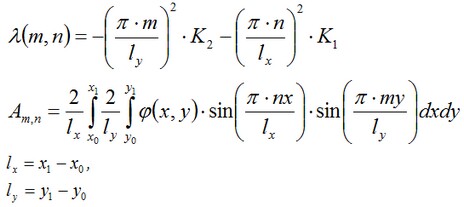
Nel nostro caso x1=100, y1=100, x0=y0=0. NOi abbiamo usato questi termini n=m=60 nell'espansione in serie.
Nei punti dati noi confronteremo la soluzione numerica ottenuta usando l'Analisi AutoFEM all'istante di tempo: 2, 10,20 sec.
|
|
Il modello ad elementi finiti con condizioni al contorno applicate e sensori localizzati alla coordinate x=20,y=20; x=20,y=80; x=80,y=20; x=80,y=80; x=50,y=50 mm |
I calcoli effettuati ci hanno permesso di ottenere i seguenti risultati:
Tabella 1. Parameters of finite element mesh
Tipo di elemnto finito |
Numero di piunti |
Numero di elementi finiti |
tetraedro lineare |
18649 |
96109 |
Tabella 2. Parameters of of time discretization
Totale tempo di calcolo (sec) |
Incremento (sec) |
Numero di strati di tempo |
10 |
0.5 |
21 |
Tabella 3. Result "Temperature"
Tempo t, s |
Soluzione numerica |
Soluzione Analitica |
Errore δ = 100% • |T* - T| / |T| |
Sensor 1-4: |
|||
2 |
29.4838 |
28.8050 |
2.36 |
5 |
13.1047 |
13.1503 |
0.35 |
10 |
4.7436 |
4.74820 |
0.10 |
Sensor 5: |
|||
2 |
55.8401 |
56.1856 |
0.61 |
5 |
35.8049 |
35.5560 |
0.70 |
10 |
13.6757 |
13.6788 |
0.02 |
|
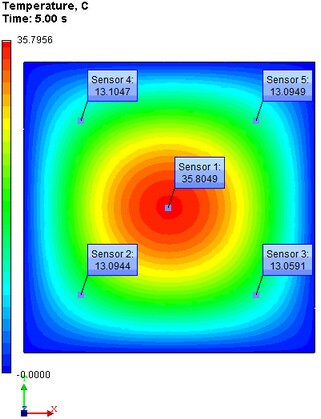
Conclusioni:
L'errore relativo della soluzione numerica confrontato con la soluzione analitica è più piccolo dello 0.9% nei 20 sec. Per il dato problema noi abbiamo ottenuto una realistica interpretazione del campo. Come avevamo già mostrato nell'esempio con il flusso di calore sulla superficie della sfera: per il calcolo su grandi intervalli di tempo è preferibile usare elementi lineari, perchè per piccoli nodi l'errore si accumula più lentamente. Nel nostro caso le conduttività termiche lungo l'asse principale della piastra sono sufficientemente alte, il che implica che esso sarà raffreddata molto veloce. Questa è la ragione perchè gli elementi quadratici su sufficientemente piccoli intervalli di tempo danno più accurati risultati. L'errore della soluzione per problemi non stazionari non eccede lo 2.5% per FE con elementi lineari e 2% con elementi quadratici.
* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.
** La soluzione è stata ottenuta dal metodo di separazione delle variabili.
Approfondire riguardo ad AutoFEM Analisi Termica
