Campo di temperatura non in regime stazionario in un cilindro isotropico

Consideriamo il problema di raffreddamento di raffreddamento di un solido cilindrico con proprietà isotropiche che ha una temperatura iniziale di t0=60 °C all'interno del volume. La temperatura di zero gradi è mantenuta ai bordi del corpo; il tempo di raffreddamento non eccede i 20 secondi. Determiniamo la temperatura nei punti di controllo 1, 2, 3 che hanno le seguenti coordinate in un sitema cilindrico (l'origine del sistema di coordinate è localizzata nel centro del cilindro): r1=25 mm, h1=25 mm; r2=25 mm, h2= - 25 mm; r3=30 mm, h3=0 mm ai seguenti instanti di tempo t1,2,3=2; 10; 20 sec.

Prametri geometrici e fisici del corpo: altezza del cilindro H =100 mm, raggio del cilindro a =50 mm. Densità ρ=7700 kg/m3, calore specifico c =460 J / (kg •°C), conduttività termica K = 40 W / (m • °C). (si veda figura).

 

Guardiamo le soluzioni per un sistema di coordiante cilindrico. Il centro del sistema di coordinate è localizzato al centro della sezione media (h è la totale altezza), e l'asse per la quale la distanza è stata misurata (r è il raggio nel sistema di coordinate cilindrico) coincide con gli assi del cilindro. Denotiamo l=H/2. Allora la soluzione dell'equazione prende la forma:

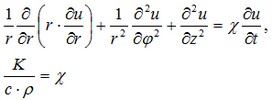
Condizioni limite per questa equazione hanno la seguente forma:

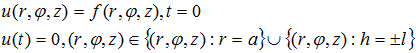
Nelle condizioni limite noi implichiamo che f è una qualche distribuzione di temperatura all'interno del corpo al momento iniziale del tempo, u(t)=0 sulla superficie del corpo cilindrico durante l'intero periodo la soluzione della data equazione nella forma di una serie di funzioni armoniche e funzioni di Bessel per il caso più generale quando f non è costante.

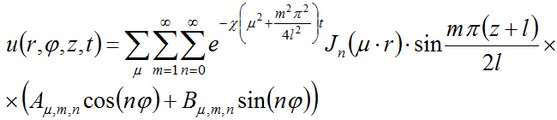
dove χ=K/(c • ρ) è il coefficiente di conduttività della temperatura, Jn (r) è la funzione di Bessel, il parametro μ è una radice dell'equazione Jn (a μ) =0

I coefficienti A e Bpossono essere calcolati in accordo con le formule mostrate qui a seguire:

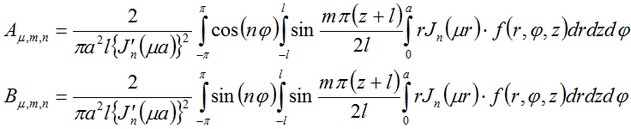
Nel nostro semplice caso quando f = t0 dall'intera serie su n noi abbiamo solo il primo termine lasciato corrispondente a n=0. Ma l'espansione su m e μ deve essere considerata. La semplificata forma della soluzione può essere scritta come:

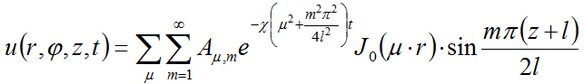
dove

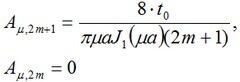
i.e., nella somma su m noi consideriamo solo i coefficienti dispari.

Confrontiamo i valori della temperatura ad un punto fissato in differenti momenti del tempo con la soluzione ottenuta dal finito elemento metodo. Il punto sarà selezionato con una sufficiente grande distanza dal principale asse del cilindro, per migliore convergenza della serie nella soluzione analitica (l'equazione ha una singolarità del tipo

1/r che significativamente afferisce alla convergenza delle funzioni della serie di Bessel).

Nei dati punti noi confronteremo la soluzione numerica ottenuta usando l'Analisi AutoFEM con la semi-analitica uno nella seguente successioni di tempi: 2, 10, 20 sec.

 

Poichè la soluzione alternativa è stata ottenuta dall'approccio semi-analitico (dalla estrazione della somma parziale della serie, esso è richiesto per determinare il numero di cifre significanti che possono essere usate per confrontare essa con la soluzione analitica. La tabella a seguire mostra con quale accuratezza i calcoli sono stati svolti per ottenerel'indicatore del relativo cambiamento nella soluzione e il fatto che al nostra serie sempre converge.

Dopo aver effettuato i calcoli i seguenti risultati sono stati ottenuti:

 

Tabella 1. Parametri degli elementi finiti della maglia

 

Tabella 2. Parametri della discretizzazione del tempo

Table 3. Result "Temperature"

 

Conclusioni:

L'errore relativo della soluzione numerica confrontata con la soluzione analitica è più piccola dello 0.9% dopo che sono trascorsi 20 s. Il calcolo dell'errore è stable nel tempo e non cresce significativimente quando il tempo computazionale è aumentato. Il grafico della temperatura dipendente mostra che la soluzione analitica e numerica coincidono. Il metodo si è rilevato essere efficace per la soluzione dei problemi con geometria complessa. Quando si usano fgli elementi quadratici il numero di nodi è significamente grande che per gli elementi lineari. Perciò, con il tempo (per ciascun nuovo strato), gli elementi quadratici sono molto più acccurati che gli elementi lineari, ma su un intervallo significativamente grande il calcolo dell'errore con elementi quadratici diventa addirittura più grande.

 

 

* I risultati dei test numerici dipendono dalla maglia ad elementi finiti e possono differire leggermente da quelli indicati nella tabella.

 

Approfondire riguardo ad AutoFEM Analisi Termica

 

 

Torna ai contenuti

autofem.com