Non-Stationary Temperature Field in an Isotropic Sphere

Let us consider a problem of determination of a temperature field inside an isotropic sphere in the volume of which we prescribe the initial temperature Tstart=293.15 oK, and which is heated along the external surface where we prescribe the constant temperature Tborder=373.15 oK (for example, the sphere at room temperature was put down to the boiling water). Let us determine the temperature at any point of the sphere (located at a distance r from the center of the sphere) in time increments equal to Δt1,2,3 = 10, 20, 30 seconds.

The sphere has the following parameters: radius a =100 mm, density of the material 7800 kg / m3, specific heat c = 440 J / (kg •oK), thermal conductivity K=50 W / (m • oK). Several alloys of steel have similar thermal characteristics.

For numerical modeling we consider a 1/8th part of the entire sphere. Conditions of symmetry are enforced by prescribing zero heat flux on the boundary surfaces of the sphere which have a center of the sphere as a vertex*2.

(see figure).

Let v be the desired solution (temperature field). Then, by taking into account that the solution does not depend on the angles of rotation of the vector emanating from the center of the sphere (symmetry condition), we can perform the change of variables in the form v=r•u, where r – distance from the center of the sphere, and u – some function. After this change of variables, we obtain the equation for u:

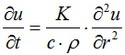
where t – is time for cooling/heating of the solid body. Boundary conditions for u:

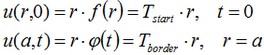
By solving this problem by the method of separation of variables, we obtain the expression for v:

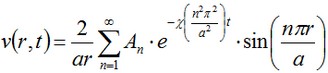
where χ=K/(c•ρ) is the coefficient of temperature conductivity. The weights An in the expansion are determined by the formula:

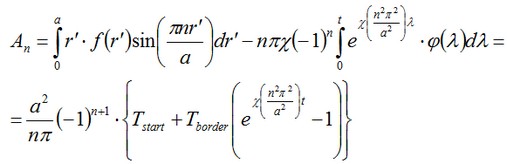
Let us compare the numerical solution with the obtained semi-analytical solution at point with radius R1=0.5 m.

In the given point we will compare the numerical solution obtained using AutoFEM Analysis with the semi-analytical one.

Since the alternative solution was obtained by the semi-analytical approach (by extraction of partial sums of the series), it is required to determine the number of significant digits which can be used for comparison with analytical solution. Table given below shows with what accuracy the calculations were carried out for obtaining solution by the series expansion and for construction of the solution plot. Conclusion about the number of significant digits in the analytical solution can be made by the indicator of the relative change in the solution and the fact that our series always converges.

After carrying out calculation the following results are obtained:

Table 1. Parameters of finite element mesh

 

Table 2. Parameters of of time discretization

Table 3. Parameters of calculation of semi-analytical solution obtained by series expansion

For numerical calculation we take the results with N=7000. For construction of plots we use the results with N=500.

Table 4. Result "Temperature"

 

 

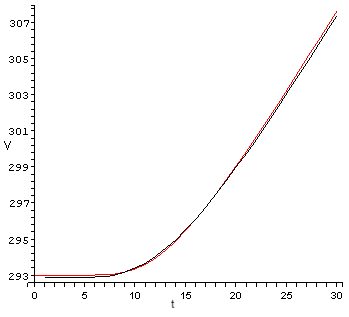
Conclusions:

We obtained realistic picture of the temperature field. The relative error of the numerical solution compared to the analytical solution does not exceed 0.03% with linear elements at t=10 s. The calculation error is stable in time and does not grow significantly when the computational time is increased. Plot of dependence of temperature on time shows that analytical and numerical solutions practically coincided.

The calculation error with quadratic elements is smaller than that with linear elements on a small interval of time.

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.

** On the boundaries where no boundary conditions are specified, the zero heat flux condition is satisfied automatically.

 

Read more about AutoFEM Thermal Analysis

autofem.com

Return to contents