Hollow Sphere Radiating Outwards

Let us consider a problem of determination of the steady-state temperature field of the hollow sphere, on the internal surface of which we maintain a constant temperature T1 =600 oK, and the external surface radiates to the ambient environment. The ambient environment has the temperature Tamb=290 oK. For this temperature the effect of radiation significantly changes the temperature inside the volume of the body. We can determine the temperature field at the control points with radii R123.

Characteristics of the sphere: external radius R=100 мм; internal radius R/2=50 mm; the thermal conductivity K=50 W/(m • oK); emissivity of the spherical surface is equal to α=1.

Let us consider a 1/8th part of the entire sphere. On the lateral surfaces of the sphere we prescribe the zero heat flux. (see figure).

Since the material is isotropic, solution of the problem will depend only on the radius. If the origin of the spherical coordinate system is placed at the center of the sphere, we will obtain the equation with boundary conditions:

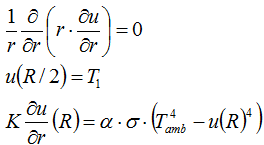
The solution of the equation has the form:

where the constants C1 and C2 are determined from the boundary conditions in the following way:

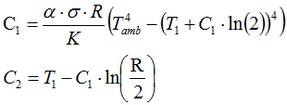
The first equation (for the given parameters) has two real roots . For the roots: C1 = -4483.400605 and C2 = -12831.06789 the solution on the boundary has the negative temperature on the boundary. For Kelvin scale it is impossible. Therefore, only the roots C1 = -13.02949201 and C2 = 560.9671302 satisfy this equation.

Let us compare the numerical solution with the obtained analytical solution at points with radii R123=0.0707106; 0.0848528; 0.0989949 m (coordinates of the sensors at these points: X123=50; 60; 70 mm and Y123=50; 60; 70 mm).

In the given points we will compare the numerical solution obtained using AutoFEM Analysis with the analytical solution.

The finite element model with applied boundary conditions

After carrying out calculation the following results are obtained:

Table 1. Parameters of finite element mesh

Finite element type	Number of nodes	Number of finite elements
linear tetrahedron	1961	7187

Table 2. Result "Temperature"

Radius r, mm	Numerical solution Temperature T*, K	Analytical solution Temperature T, К	Error δ = 100%* \|T* - T\| / \|T\|
0.0707106	585.6841	595.4843221	1.65
0.0848528	588.1666	593.1087648	0.83
0.0989949	591.5466	590.9686443	0.10

Conclusions:

The relative error of the calculations approaches 1.65%. Notice that when the mesh is refined, the numerical solution approaches the analytical solution slower because of the non linearity of the problem itself.

As we see, when computing the radiation, the relative error is practically the same for linear and quadratic elements. This can be explained by the error in the solution of the nonlinear equations. Thus, when computing radiation, it makes sense to use only linear elements because of smaller computational cost.

* The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.

** Roots were found with the help of the Maple 9.5 system.

autofem.com

Return to contents