Point Power Source inside the Sphere

Let us consider a problem of finding a temperature field inside the isotropic sphere with a point source in the center. The temperature is held constant on the spherical surface.

Radius of a sphere that bounds the body is R=0.1 m; the temperature on the surface of a sphere is t=293.15 oK. The center of the sphere coincides with the origin of the coordinate system. Let us assume that at the center of the sphere a heat point source of power ρ=500 W is prescribed. Coordinates of the point source are equal to P0=(0, 0, 0). Thermal conductivity is assigned the value equal to λ=1 W/(m•oK). [new material with thermal conductivity = 1].

For modeling we consider a 1/8th part of the sphere. In the numerical model we apply the power of 500 W, and thus we divide it by 8, i.e., 500 / 8 = 62.5 W.

(see figure).

For a given problem an exact solution at the point P=P(x, y, z) can be found as:

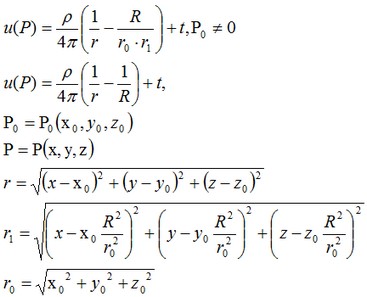
The function u is a solution of the differential equation and can be written in the form:

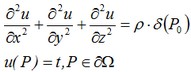
where δ is Dirac δ-function, Ω – domain of the sphere, ∂Ω – boundary of the sphere.

Steady-State Temperature of a Multilayer Wall, the finite element model with applied temperatures

The finite element model with applied boundary conditions

Let us compare analytical solution with the solution obtained from AutoFEM. After carrying out calculation the following results are obtained:

Table 1. Parameters of finite element mesh

Finite element type	Number of nodes	Number of finite elements
linear tetrahedron	1141	3903

Table 2. Result "Temperature"

Distance from the center, mm	Numerical solution Temperature T*, K	Analytical solution Temperature T, К	Error δ = 100%* \|T* - T\| / \|T\|
R 30	1215.614	1221.553	0.49
R 40	896.289	889.981	0.71
R 50	702.936	691.037	1.72
R 60	562.766	558.408	0.78

Steady-State Temperature of the Multilayer Wall, temperature distribution

Conclusions:

The relative error of the numerical solution compared with the analytical solution not exceed 1.8% for linear elements.

The method was proven to be effective for solving problems with point sources and singularities in the solution.

Furthermore note that near singular sources (concentrated on the edge or at the point), the relative error is higher than at the points more remote from the sources. This happens because the temperature at these sources is equal to infinity.

*The results of numerical tests depend on the finite element mesh and may differ slightly from those given in the table.

autofem.com

Return to contents