 |
AutoFEM Analysis Statik Analyse | ||||||
Statik Analyse
Das Hauptziel der Statikanalyse von Strukturen ist die Evaluation der Belastungen einer Struktur unter konstanten Belastungen. Die Analyse der Belastungszustände wird üblicherweise mit dem Ziel durchgeführt, die Produktmerktmale, wie deren Stärke bei statischen Belastungen zu erforschen. Das Stärkekriterium wird in der Regel wie folgt formuliert:
Die Belastung σ , die sich in einer Struktur unter externen Kräften entwickelt muss weniger als die Sicherheitsbelastung [ σ ], für das gegebene Material nach der Bestimmung der Marge des
Sicherheitsfaktors, betragen.
![]()
Das statische Analysemodul von AutoFEM dient der Berechnung der statischen Belastungszustände einer in AutoCAD erstellten 3D-Struktur. Das Analysemodul verwendet die AutoCAD-Modelle direkt und benötigt keine zusätzlichen Schritte, um das Modell vorzubereiten.
Die Hauptresultate der Statikanalyse sind:
| • | Verschiebungsfeld der Struktur in Knoten des Finite-Elemente-Netzes ; |
| • | Spannungsfeld |
| • | Feldkomponente der Belastung; |
| • | Deformationsenergie; |
| • | Knotenkräfte; |
| • | Felddistribution des Sicherheitsfaktors; |
Diese Daten sind normalerweise genug, um das Verhalten der Struktur vorherzusagen. Mit deren Hilfe können Entscheidungen bezüglich der Optimierung der Struktur zur Garantie der genügenden Stärke des Objekts getroffen werden.
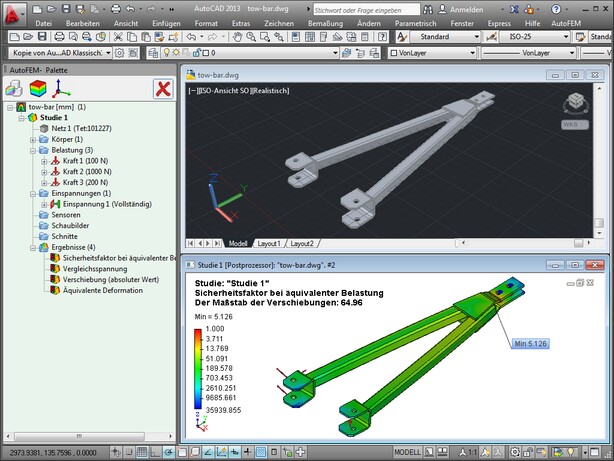
Details der statischen Analyse: Schritte
Eine statische Analyse eines Modells erfolgt in mehreren Stufen. Gelistet sind die Elemente, für die Durchführung einer Analyse erforderlich sind.
Um eine statische Analyse zu starten, führen Sie die folgenden Schritte aus:
Schritt 1. Ein 3D-Modell einer Struktur kreieren.
Bevor Sie in AutoFEM zu arbeiten beginnen, sollten sie ein 3D-Modell vorbereitet haben, welches sie untersuchen wollen. Ein solches kann in der AutoCAD Umgebung erstellt oder von einem anderen System importiert werden. Die statische Analyse kann mit einem oder mehreren Körpern geschehen.
Schritt 2. "Studie" erstellen.
Sie können eine der folgenden Möglichkeiten benutzen, um eine Studie zu erstellen:
Kommando: |
_FEMASTUDY |
Hauptmenü: |
AutoFEM | Studie erstellen... |
Symbol: |
|
Sie müssen auch den Typ der Studie ("Statische Analyse") im Eigenschaftsfenster angeben. Falls mehrere Körper im Raum sind, müssen Sie einen oder mehrere (angrenzende) davon selektieren, für welche Sie die Studie wollen.
Schritt 3. Material definieren.
Einer der erforderlichen Elemente für jede Berechnung ist das Material. Eine detailierte Beschreibung der Methoden zur Materialdefinition ist im Kapitel des Preprozessors beschrieben.
Schritt 4. Netz kreieren.
Um die Finite-Elemente-Modellierung durchzuführen, müssen Sie das Finite-Elemente-Netz kreieren.Standardmäßig beginnt die Netzkonstruktion von selbst, wenn Sie eine neue Studie kreieren. Der Nutzer kann aber auch ein Netz mit dem AutoFEM Kommando " AutoFEM | Netz erstellen..." kreieren. Dabei können Sie verschiedene Parameter der Diskretisierung des Modells definieren. Das Finite-Elemente-Netz kann signifikanten Einfluß auf die Qualität der Resultate in komplexen Situationen haben. Die Parameter der Netzgenerierung werden im Detail in den entsprechenden Kapitel des AutoFEM Preprozessors beschrieben.
Schritt 5. Randbedingungen anwenden.
In der statischen Analyse sind Randbedingungen durch Restriktionen und externen Belastungen des Systems dargestellt. Die Randbedingungen sind äußerst wichtig und setzen ein gutes Verständnis der zu lösenden Studie voraus. Aus diesem Grund müssen die Eigenschaften der Studie sehr genau durchdacht werden bevor sie gelöst mit AutoFEM Analyse gelöst wird. Die Restriktionen zu definieren ist eine Voraussetzung für die Durchführung einer korrekten statischen Analyse. Die kombinierten Restriktionen auf die Bewegung des Objekts muss folgende Bedingungen erfüllen:
Um für eine statische Analyse geeignet zu sein, muss ein Modell Restriktionen haben, welche die freie Bewegung im Raum verhindern. Wird diese Bedingung nicht erfüllt wird falsche Resultate oder einen Abbruch der Berechnung zur Folge haben.
Ein Kommando steht in AutoFEM zur Verfügung um Restriktionen einzuführen: "Einspannungen". Der Typ "Allgemeine Beschränkung" definiert eine totale Fixierung (unbeweglich) des ausgewählten Elements. Der "Allgemeine" Typ der Restriktion erlaubt es, das Element entlang der Achsen des ausgewählten Koordinatensystems zu limitieren.
Der Befehl "Einspannung" hat noch eine andere nützliche Funktion: Es gibt die Möglichkeit bekannte Verschiebungen für die Struktur anzugeben. Dafür muss der Wert der fixierten Verschiebung des Elements entlang einer oder mehreren Achsen des Koordinatensystems in das "Einspannungen"-Eigenschaftsfenster eingegeben werden.
Die statische Analyse wird mit diesen Bedingungen durchgeführt. Beachten Sie dass eine statische Lösung ohne zusätzlichen Kräfte möglich ist Auf diese Art kann man die Entwicklung der Belastungen in einer belasteten Struktur untersuchen, wenn die quantitativen Werte der Belastung bekannt sind.
|
|
Beispiel für die Verwendung bekannter Verschiebungen |
|
AutoFEM bietet eine Reihe spezieller Befehle zur Definition der Belastungen: Diese erlauben die Haupttypen von Belastungen (Kraft, Druck, Fliehkraft, Beschleunigung, Last, Drehmoment) einzusetzen. Detaillierte Beschreibungen aller Typen finden Sie im Kapitel des Preprozessors. Beachten Sie eine zusätzliche Funktion in der statischen Analyse von AutoFEM: Der Benutzer kann Belastungsanalysen einer Struktur nicht nur mit diversen Kräften durchführen, aber auch mit thermischen Belastungen (die Thermoelastizitätsstudien) Wie bekannt verändern sich Materialien und Strukturen unter Temperaturbelastungen: Sie dehnen sich unter Hitze aus und schrumpfen unter Kälte. Veränderungen in den Dimensionen eines Körpers verändert auch die Belastungen. AutoFEM berücksichtigt Temperaturveränderungen. Um die Temperaturen zu definieren, bei transiente Temperaturfelder, benutzen Sie eine dieser Möglichkeiten:
Kommando: |
_FEMATEMP |
Hauptmenü: |
AutoFEM | Belastungen/Einspannungen | Temperatur... |
Symbol: |
|
Gleichzeitig müssen Sie die Option "Thermoeffekte beachten " unter [Thermoelastizität] in den Studienparameter wählen, um die thermischen Belastungen zu berücksichtigen. Sie müssen ebenfalls die Temperatur der Nullbelastung definieren, bei welcher keine Belastungen auf das Objekt wirken und das Temperaturfeld bestimmen (Details dazu finden Sie im Kapitel "Einstellungen des Linearen Statik Prozessors")
Schritt 6. Berechnungen ausführen.
Ist das Finite-Elemente-Netz für das Modell erstellt und die Randbedingungen (Restriktionen und Belastungen) angewandt, können Sie den Prozess der Lösung der algebraischen Gleichungssysteme der statischen Analyse beginnen. Nutzen Sie eine dieser Möglichkeiten, um die Berechnungen zu beginnen.
Kommando: |
_FEMASOLVE |
Hauptmenü: |
AutoFEM | Lösen... |
Symbol: |
|
Die Berechnung kann vom Kontextmenü mit Rechtsklick ![]() auf den Namen der gewählten Studie im Studienbaum gestartet werden. Standardmäßig öffnet sich der Dialog "Studienparameter" automatisch vor der Berechnung. Dieser Dialog ermöglicht es die gewünschten Optionen und Eigenschaften der Resultate, sowie die Angabe der anzuzeigenden Lösungen und Eigenschaften.
auf den Namen der gewählten Studie im Studienbaum gestartet werden. Standardmäßig öffnet sich der Dialog "Studienparameter" automatisch vor der Berechnung. Dieser Dialog ermöglicht es die gewünschten Optionen und Eigenschaften der Resultate, sowie die Angabe der anzuzeigenden Lösungen und Eigenschaften.
Detailliertere Beschreibungen der Studieneigenschaften finden Sie im Kapitel "Einstellungen des Linearen Statik Prozessors". Die meisten Einstellungen werden vom Prozessor automatisch gewählt, abhängig von den Dimensionen der Studie und der Randbedingungen. Klicken Sie den Knopf [OK] im Studienparameter Dialog, um den Prozess der Berechnung der algebraischen Gleichungssysteme zu beginnen.
Die Stufen der Berechnung der Gleichungen und zusätzlichen Informationen werden in einem speziellen Informationsfenster angezeigt. Klicken Sie auf [Schließen] in diesem Informationsfenster wir die Berechnung abgebrochen. Das Aktivieren von "Schließen Sie dieses Dialogfeld nach der Berechnung" wird die Schließung des Informationsfensters automatisch nach der Berechnung erzwingen. "Dokument nach der Berechnung zu Speichern" wird die Resultate der Berechnungen und alle aktiven Daten automatisch speichern.

Die folgende Referenzdaten werden im Informationsfenster ausgegeben:
Knoten - Die Anzahl Knoten im Finite-Elemente-Netz.
Elemente - Die Anzahl Tetraeder im Finite-Elemente-Netz.
Argumente - Die Anzahl Gleichungen der linearen Statik.
Berechnungsmethode - Der Benutzte Algorithmus zur Berechnung der Gleichungen. Die verschiedenen Arten von Algorithmen und deren Nutzen ist im Kapitel "Einstellungen des linearen Statik Prozessors"
Lösung gefunden – stellt fest, dass das System erfolgreich berechnet wurde. Es gibt auch Zusatzinformationen in den Klammern: iter – Anzahl der Ausgeführten Iterationen (falls die iterative Methode benutzt wurde) und tol – Fehlberechnungen des Resultats nach der Berechnung
Beim Iterationsrechner wird die Nummer der aktuellen Iteration und die Restfehlerquote der Lösung gezeigt. In der direkten Methode ist es der Prozentsatz der gesamten gelösten Gleichungen. Der Anwender kann in Echtzeit sehen, was die Lösungsrate der Gleichungen ist und den Prozess überwachen. Zusätzlich sind für beide Methoden drei Parameter vorhanden, welche die Belastung des Arbeitsspeichers anzeigen: Wieviel davon von den Berechnungen aktuell genutzt wird, die maximale Nutzung und wieviel verfügbar ist. Diese Information erlaubt es dem Nutzer zu entscheiden, ob sein Computersystem passend zur Berechnung dieser Studie ist.
Die Berechnungsschritte werden ebenfalls als dynamische Leiste visuell angezeigt. Zusätzlich ist die seit Beginn verstrichene Zeit sichtbar. Nach dem Abschluß der Berechnungen muss der Nutzer das Fenster schließen. (außer wenn die automatische Schließung aktiviert wurde)
Schritt 7. Analyse der Statik Resultate.
Nach dem Abschluß der Berechnungen erscheint ein neuer "Resultate" Ordner im Studienbaum. Standardmäßig zeigt er die Resultate, die unter "Resultate" der Studieneigenschaften vorgegeben wurden. Insgesamt kann der Benutzer 38 Resultate, in 6 Gruppen sortiert, anzeigen lassen.
Die Gruppe "Verschiebung" beinhaltet folgende Resultate:
![]() - Komponente des Verschiebungsvektors für ein Knoten des Finite-Elemente-Netzes entlang der OX-Achse des globalen Koordinatensystems.
- Komponente des Verschiebungsvektors für ein Knoten des Finite-Elemente-Netzes entlang der OX-Achse des globalen Koordinatensystems.
![]() - Komponente des Verschiebungsvektors für ein Knoten des Finite-Elemente-Netzes entlang der OY-Achse des globalen Koordinatensystems.
- Komponente des Verschiebungsvektors für ein Knoten des Finite-Elemente-Netzes entlang der OY-Achse des globalen Koordinatensystems.
![]() - Komponente des Verschiebungsvektors für ein Knoten des Finite-Elemente-Netzes entlang der OZ-Achse des globalen Koordinatensystems.
- Komponente des Verschiebungsvektors für ein Knoten des Finite-Elemente-Netzes entlang der OZ-Achse des globalen Koordinatensystems.
Verschiebung, absoluter Wert – Der Absolute Wert der Knotenverschiebung des Modells, definiert für jeden Knoten entsprechend der Formel: ![]() , wobei x, y, z -Verschiebungsvektors Komponente sind für den i-ten Knoten des Finite-Elemente-Netzes.
, wobei x, y, z -Verschiebungsvektors Komponente sind für den i-ten Knoten des Finite-Elemente-Netzes.
Die Gruppe «Spannungen» beinhaltet folgende Resultate:
![]() - relative Vergleichsspannung ausgewertet von Komponenten des Spannungstensor gemäß der Formel:
- relative Vergleichsspannung ausgewertet von Komponenten des Spannungstensor gemäß der Formel:![]() ;
;
![]() - Hauptspannung in der Richtung der OX-Achse des globalen Koordinatensystem;
- Hauptspannung in der Richtung der OX-Achse des globalen Koordinatensystem;
![]() - Hauptspannung in der Richtung der OY-Achse des globalen Koordinatensystem;
- Hauptspannung in der Richtung der OY-Achse des globalen Koordinatensystem;
![]() - Hauptspannung in der Richtung der OZ-Achse des globalen Koordinatensystem;
- Hauptspannung in der Richtung der OZ-Achse des globalen Koordinatensystem;
![]() - Druckspannung in Richtung der OY-Achse des globalen Koordinatensystems auf einer Ebene mit dem Normalvektor parallel zu der OX-Achse ist;
- Druckspannung in Richtung der OY-Achse des globalen Koordinatensystems auf einer Ebene mit dem Normalvektor parallel zu der OX-Achse ist;
![]() - Druckspannung in Richtung der OZ-Achse des globalen Koordinatensystems auf einer Ebene mit dem Normalvektor parallel zu der OX-Achse ist;
- Druckspannung in Richtung der OZ-Achse des globalen Koordinatensystems auf einer Ebene mit dem Normalvektor parallel zu der OX-Achse ist;
![]() - Druckspannung in Richtung der OZ-Achse des globalen Koordinatensystems auf einer Ebene mit dem Normalvektor parallel zu der O>-Achse ist;
- Druckspannung in Richtung der OZ-Achse des globalen Koordinatensystems auf einer Ebene mit dem Normalvektor parallel zu der O>-Achse ist;
![]() - Hauptspannung
- Hauptspannung ![]() .
.
Spannungsintensität wird in folgender Weise definiert:![]()
Fehlerschätzung der Spannung: Dieses Resultat zeigt eine prozentuale Schätzung der Fehlberechnungen. Die Schätzung wird als Elementwert dargestellt (konstant in einem Tetraeder). Ein großer Wert bedeutet, dass es einen großen Unterschied der Spannung zu den benachbarten Elementen gibt. Das zuverlässigste Ergebnis der Spannungsberechnung wird erreicht, wenn die Fehlerschätzung zu einer gleichmässigen Verteilung neigt. Für mehr Informationen zur Fehlerschätzung, verweisen wir gerne auf International Journal for Numerical Methods in Engineering, vol. 24, 337-357 (1987) “A Simple Error Estimator and Adaptive Procedure for Practical Engineering Analysis” von O.C. Zienkiewicz und J. Z. Zhu)
Die Gruppe «Belastungsgrenze zu Sicherheitsfaktor» beinhaltet folgende Resultate:
Sicherheitsfaktor bei äquivalenter Belastung steh für das Verhältnis der zulässigen Belastung eines Materials [σ ] zur äquivalenten Belastung.
![]()
Sicherheitsfaktor bei tangierender Belastung wird mit folgender Formel berechnet:
![]()
Sicherheitsfaktor bei normaler Belastung wird mit folgender Formel berechnet:
![]()
Die Grenzbelastung eines Materials ist in den Materialeigenschaften der AutoCAD Bibliothek oder im entsprechenden Feld der Studienbibliothek definiert. Die Dehngrenze wird als Grenzbelastung für Plastikmaterialien akzeptiert.
Die Gruppe «Deformation» beinhaltet folgende Resultate:
![]() - relative äquivalente Deformationen in Bezug auf Komponenten des Verzerrungstensors durch die Formel:
- relative äquivalente Deformationen in Bezug auf Komponenten des Verzerrungstensors durch die Formel:
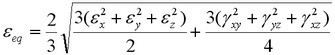 ;
;
![]() - Kompressive Deformationen auf der OX-Achse des globalen Koordinatensystems;
- Kompressive Deformationen auf der OX-Achse des globalen Koordinatensystems;
![]() - Kompressive Deformationen auf der OX-Achse des globalen Koordinatensystems;
- Kompressive Deformationen auf der OX-Achse des globalen Koordinatensystems;
![]() - Kompressive Deformationen auf der OX-Achse des globalen Koordinatensystems;
- Kompressive Deformationen auf der OX-Achse des globalen Koordinatensystems;
![]() - Schubdeformationen in der OXY Ebene;
- Schubdeformationen in der OXY Ebene;
![]() - Schubdeformationen in der OXZ Ebene;
- Schubdeformationen in der OXZ Ebene;
![]() -Schubdeformationen in der OYZ Ebene;
-Schubdeformationen in der OYZ Ebene;
![]() -Hauptdeformationen
-Hauptdeformationen ![]() .
.
Deformationsenergiedichte. Das Ergebnis spiegelt die Volumenverteilung der Deformationsenergie über das Modell wieder.
Die Gruppe «Knotenkräfte». Diese Resultate zeigen die Kräfte, die sich in den fixen Knoten des Finite-Elemente-Modells bilden.
![]() - Knotenkräfte auf der OX-Achse des globalen Koordinatensystems;
- Knotenkräfte auf der OX-Achse des globalen Koordinatensystems;
![]() - Knotenkräfte auf der OY-Achse des globalen Koordinatensystems;
- Knotenkräfte auf der OY-Achse des globalen Koordinatensystems;
![]() - Knotenkräfte auf der OZ-Achse des globalen Koordinatensystems;
- Knotenkräfte auf der OZ-Achse des globalen Koordinatensystems;
Knotenkräfte (absoluter Wert) – Die Amplitude des absoluten Wert der Knotenkräfte des Modells definiert als:![]() , wobei
, wobei ![]() - die x-Komponente,
- die x-Komponente, ![]() - die y- Komponente und
- die y- Komponente und ![]() - die z-Komponente der Knotenkräfte am i-ten Knoten des Finite-Elemente-Netzes ist.
- die z-Komponente der Knotenkräfte am i-ten Knoten des Finite-Elemente-Netzes ist.
Die Gruppe “Totale Belastung” zeigt die angewandten Belastungen des Finite-Elemente-Modells als effektive Reaktion der Knoten. Dieser Typ von Daten entspricht Referenzinformationen.
Temperatur. Dieses Resultat zeigt die Temperaturverteilung auf dem Volumen des Modells.
Algorithmus der statischen Analyse

Algorithmus der statischen Stärke basierend auf dem modellieren.
Wenn die Berechnung der Studie erfolgreich abgeschlossen wurde, können Sie die erhaltenen Resultate analysieren, um Schlüsse über die statische Stärke der Struktur ziehen zu können. in den meisten Fällen reichen drei Typen der Resultate: Verschiebungen, Spannungen und der Sicherheitsfaktor. Eine typische Vorgehensweise, um die Resultate zu analysieren ist die folgende:
1. Analyse der Verschiebung. Im Studienbaum klicken Sie auf "Öffnen" oder "In neuem Fenster öffnen" im Kontextmenü, um "Verschiebungen (absoluter Wert) zu öffnen. Sie können dort visuell das Muster und den Bereich der Verschiebung der Struktur untersuchen. Es ist nötig die Verschiebungen zu analysieren, um die Richtigkeit der angewandten Belastungen und damit auch die Korrektheit der daraus berechneten Lösung, zu erkennen. Wenn eine Lösung gefunden wurde und die Belastungen wie erwartet dargestellt sind, können Sie den nächsten Schritt vornehmen:
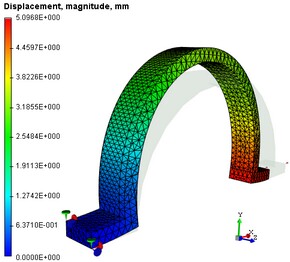
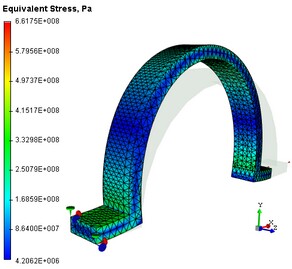
Das Diagramm der absoluten Verschiebungen und tangentialspannung
2. Analyse der Spannung. Öffnen sie das Resultat "tangentialspannung". Sie können visuell die Muster der Berechnung untersuchen. Der Farbmaßstab hilft den ungefähren Wert des angezeigten Resultats anzuzeigen. Wenn sie die Maus über das Modell bewegen und Doppelklicken, wird der genaue Wert an dieser Stelle angezeigt. Die "Tangentialspannung" läßt folgende Schlüsse zu:
a) Feststellen, an welchen Orten und welche Elemente des Modells die größte Spannung aushalten;
b) Mit dem Vergleich der Maximalspannung mit der Zulässigen aus den Materialeigenschaften können Sie die Strukturstärke beurteilen.
3. Schätzung des Sicherheitsfaktors. Öffnen Sie das "Sicherheitsfaktor bei äquivalenter Belastung"-Resultat.
Dieses Resultat ermöglicht die Schätzung der quantitativen Rate der sicheren Belastung zur berechneten äquivalenten Belastung der Materialeigenschaften. Standardmäßig werden die Resultate in einer logarithmischen Skalierung angezeigt, um die Farbskala zu vereinfachen. Nähert sich die Rate der sicheren und berechneten Belastung eins oder wird sie kleiner als eins, dann muss das Objekt optimiert werden, da es der erforderlichen Stärke nicht entspricht.
Einstellung des linearen und nichtlinearen Statikprozessors
Die benutzerdefinierten Studieneigenschaften werden zusammen mit dem Dokument gespeichert und bei einer Kopie der Studie übernommen. Der Hauptgrund der Studieneigenschaften sind die Einstellungen des Prozessors, die gewünschte Anzeige der Resultate und die deskriptiven Informationen der Studie wie Kommentare oder die Bezeichnung. Die Parameter der statischen Analyse haben fünf Tabs:
Unter [Allgemein] können Sie die deskriptiven Eigenschaften einfügen.

Unter "Bezeichnung" kann der Nutzer den Namen der Studie wählen. Dieser Name wird im Studienbaum, um Resultatefenster, und im Bericht erscheinen.
Bei "Typ" wird der Studientyp definiert. Beachten Sie, dass AutoFEM es erlaubt, den aktuellen Studientyp einfach zu verändern. Zum Beispiel kann der Nutzer zuerst eine statische Analyse durchführen und dann den Typ zu "Frequenzanalyse" wechseln. Bei "Kommentar" kann ein freier Text eingefügt werden mit Informationen zur Studie.
Diese Eingabe wird im Bericht der Studie eingefügt.
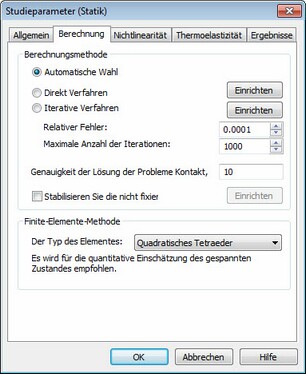
Unter [Berechnung] können Sie die Prozessoreigenschaften für die Lösung der statischen Analyse bestimmen
Die Kontrollelemente unter "Berechnungsmethode" lassen Sie die Methode der Lösung der algebraischen Gleichungen bestimmen.
Automatische Wahl. Das System wählt die Methode abhängig von der Anzahl der zu lösenden Gleichungen. Ist die Zahl größer als die in den Kontoeinstellungen von AutoFEM festgelegten (standardmäßig 100'000) wird das System die Berechnung mit der iterativen Methode durchführen. Ist sie kleiner, benutzt es die direkte Methode.
Direkte Methode. Die Gleichungssystem werden anhand der Gauss-Methode via LU-Faktorisierung der Steifheitsmatrix gelöst. Diese Methode ist effektiv, um Gleichungssysteme zu lösen, die auf linearen Finite-Elemente basieren. In einigen Fällen wird die direkte Methode auch benutzt, um Analysen von Systemen mit quadratischen Finite-Elementen durchzuführen. Sie kann statt der iterativen Methode verwendet werden, wenn der iterative Algorithmus nicht zu einer stabilen Lösung konvergiert, oder wenn das Konvergenztempo sehr langsam ist (mehrere tausend Iterationen) Diese Situation ergibt sich für "dünne" Studien (Das Modell ist flach oder gestreckt) oder wenn die Anzahl der Finite-Elemente sehr groß ist und sie sich sehr von equilateralen Elementen unterscheiden (wenn das Verhältnis der Länge des Elementecken in die Hunderte oder Tausende gehen). Zusätzliche Einstellungen zur direkten Methode sind verfügbar ("Optionen")
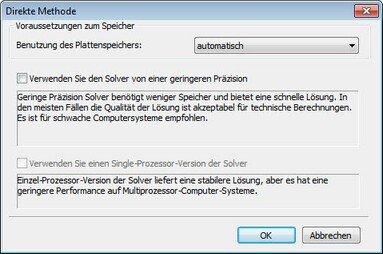
Iterative Methode. Die Gleichungssysteme werden mit der iterativen Methode gelöst. Diese Methode wird standardmäßig bei Gleichungssystemen basierend auf quadratische Finite-Elemente angewandt. Die folgenden zwei Optionen können für die iterative Methode benutzt werden: die relative Toleranz und die maximale Nummer an Iterationen. Zusätzliche Einstellungen der Methode sind unter "Optionen" verfügbar.

Zusätzliche Nutzung des Festplattenspeichers
Der Anwender kann auch die Interaktion mit dem externen Speicher des Computers kontrollieren, wenn Gleichungssysteme mit der direkte und der iterativen Methode gelöst werden. Es gibt drei Optionen, wie der Festplattenspeicher zusätzlich benutzt werden kann: automatisch, verboten, zwangsweise. Die Nutzung des zusätzlichen Speicher erlaubt es, die Zersetzung der Steifheitsmatrix zu speichern und ist nötig, wenn die für die Berechnung nötige Leistung höher als der Verfügbare Arbeitsspeicher. Beachten Sie, dass die Berechnungszeit bei großen Studien mit vielen Dimensionen signifikant sein kann mit dem Einsatz des Festplattenspeichers, da viele Lesen-Schreiben Sequenzen ausgeführt werden müssen. Es wird auch ein großer Speicher benötigt (bis zu mehreren Gigabyte). Stellen Sie sicher, dass Sie genügend Speicherplatz haben bevor Sie mit der Lösung der Studie beginnen.
Verhindert der Nutzer die Möglichkeit der Nutzung des Festplattenspeichers bei komplexen Berechnungen, kann dies zum Abbruch der Berechnung führen, wenn der benötigte Speicher für die Zersetzung der Matrix zwei Gigabyte erreicht (für Windows 32-Bit)
Die Option einen Solver von geringeren Präzision zu benutzen.
Dieser Modus benötigt nur ungefähr zwei drittel des Arbeitsspeicher und führt die Berechnungen schneller aus. In den meisten Fällen reicht diese Berechnung für technische Kalkulationen. Diese Option kann eingesetzt werden, wenn der Benutzer einen nicht sehr leistungsfähigen Computer besitzt. Standardmäßig wird der normale Solver benutzt. Es ist ebenfalls möglich, den Solver im Einzel-Prozessor Modus zu wählen.
Typ des Vorkonditionierer (für die iterative Methode). Vier Typen von Vorkonditionierer sind verfügbar. der Kombinierte Vorkonditionierer ist der schnellste und Standardmässige. Er benötigt am meisten Speicher. Unvollständige Dekompositionierung benötigt mehr Speicher, nämlich soviel wie die Steifheitsmatrix. Der diagonale und Identität Vorkonditionierer benötigen praktisch keine zusätzlichen Speicher, aber bieten die tiefste Konvergenzrate.
Relative Genauigkeit - die Genauigkeit der iterativen Lösung je kleiner die angegebenen Fehlkalkulationen, desto größer die Anzahl Schritte (Iterationen), die nötig sind.
Maximale Anzahl an Iterationen - die kritische Anzahl an Iterationen, nach welchen die Lösung der Gleichungssysteme beendet wird, auch wenn die gewünschte Präzision nicht erreicht wurde.
Genauigkeit der Kontaktrestriktionen. Dieser Parameter zeigt den Prozentsatz von sich berührenden Knoten, welche bei jedem Schritt der Berechnung ausgeschlossen werden. Der Mindestwert ist 1%, der Maximalwert 50%. Aus der Sicht der Nutzer verlangsamt ein kleinerer Wert die Lösung des Problems, auch wenn die Genauigkeit der Lösung erhöht wird.
Stabilisierung des unfixierten Modells. Normalerweise ist die Statik Analyse eines unfixierten Modells, welches nur von den Kräften balanciert ist, unmöglich. Wegen Rundungsfehlern ist das Modell im Raum verschoben oder rotiert. Diese Verschiebungen sind signifikant größer als Deformationen, die im Modell wegen der statischen Kräften und erlauben es nicht, die Belastungen des Systems zu untersuchen. Die Stabilisation des unfixierten Modells im Raum ändert dies. Das Prinzip der Stabilisation ist wie folgt: Auf allen Oberflächen des Modells werden imaginäre Federn angebracht. Es wird angenommen, dass die Steifheit der Federn vernachlässigbar sind im Vergleich mit der Steifheit des Materials des Objekts. Deswegen beeinflussen sie das Resultat nicht signifikant. Diese Federn erlauben es aber dem Modell nicht sich unkontrolliert im Raum zu bewegen. Der Nutzer kann einen akzeptablen Wert für die Steifheit der Stabilisation des System für jeden praktischen Fall wählen.
Finite-Elemente Methode. Standardmäßig benutzen alle Berechnungen eine quadratische Approximation von Verschiebungen, egal welcher Art die Finite-Elemente-Netze sind. Ist der Nutzer nur an qualitativen Ergebnissen, also nur an die relative Verteilung der Spannungsfeldern interessiert, sollte er statt eines feinen Netzes die lineare Elemente Lösung benutzen, welche viel schneller ist als die quadratische Approximation. Dieses Hybridelement kann für die statische Analyse der Modelle mit linearen plattenähnlichen-, aber auch 3D Volumen genutzt werden.
Die Analyse mit Tetraedrisch linearen Elemente ist teilweise zu ungenau für quantitative Resultate. Die Maximale Verschiebung und die Spannungen sind viel kleiner mit der Berechnung via der linearen tetraedrischen Finite-Elemente. Die viel genauere Methode ist die quadratische Elemente Berechnungsmethode für quantitative Resultate (Die Standardmethode)

Unter [Thermoelastizität] kann die Methode zur Berechnung von thermischen Belasten definiert werden.
Thermoeffekte beachten. Berücksichtigt den Kalkulationsmodus welcher Belastungen, welche sich durch lineare Expansionskräfte bei Hitze im Körper miteinbezieht.
.
Temperatur der Nulldeformation: - die Anfangstemperatur des Körpers, bei welcher keine thermische Belastung wirkt. Der Benutzer kann die Temperaturwerte auf den folgenden Skalen auswählen: K - Kelvin; C - Celsius; F- Fahrenheit.
Die Spezifizierung der thermischen Belastungen findet in der Gruppe "Temperaturfelder" statt.
Konstante Temperatur: - Der Wert eines konstanten Temperaturfeld und die Einheit welche die ganze Studie betreffen.
Voreingestellte Temperatur verwenden: - Thermische Belastungen, die mit dem Kommando:"AutoFEM | Belastungen/Einspannungen | Temperatur" bestimmt wurden.
Resultate der Thermischen Analyse verwenden: - Verfügbare Ergebnisse der thermischen Analyse werden für die Definition der thermischen Belastungen verwendet. In der Aufklappliste können Sie den Namen der gelösten Studie und (wenn nötig) den Zeitpunkt wählen. Beachten Sie, dass einige Bedingungen erfüllt sein müssen, damit die Resultate benutzt werden können:
1. Identitätsbedingung des Finite-Elemente-Netzes in beiden thermischen Analysen. Der einfachste Weg, diese Identität zu erreichen ist die "kopieren"-Funktion im Kontextmenü. Die Sequenz der auszuführenden Schritte ist die folgende:
a) Kreieren Sie eine Studie des Typs "Thermische Analyse", generieren Sie ein Netz, definieren Sie Randbedingungen und führen Sie sie aus. Es wird angenommen, dass die berechneten Temperaturen zur Definition der Ursprungstemperaturen einer anderen Studie (transiente thermische Analyse) benutzt werden.
b) Machen Sie eine Kopie der Studie mit dem Befehl "kopieren"
c) Definieren Sie Grenzbedingungen einer transienten thermischen Studie . Unter "Parameter" der Studieneigenschaften wählen Sie den Namen der ersten Studie, und falls es eine transiente Analyse ist, den gewünschten Zeitpunkt.
Als Resultat haben wir zwei Studien mit verschiedenen Typen, aber mit gleichem Finite-Elemente-Netz.
2. Die Eigenschaft "Berechnung mit linearen Elementen" unter "Berechnung" der Studienparameter sollte die gleichen Eigenschaften in beiden Studien haben. Zum Beispiel, wenn die erste thermischen Analyse aus linearen Elementen gemacht ist, dann kann die zweite, auf der ersten basierenden, thermische Analyse ebenfalls nur aus linearen Elementen bestehen.
Beachten Sie dass die Berechnung einer transienten Wärmetransferstudie mehr CPU Zeit benötigt im Vergleich zu stationären Studien, weil das algebraische Gleichungssystem für jeden vom Nutzer gewählten Zeitpunkt gelöst werden muss.
Unter [Resultate] können Sie die Resultate-Typen, die im Studienbaum angezeigt werden sollen definieren.
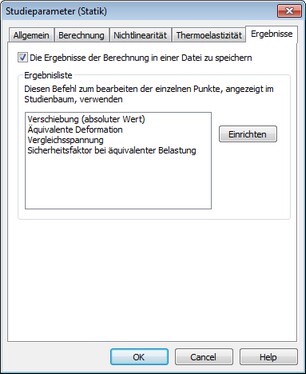
Die Ergebnisse der Berechnung in einer Datei speichern. - Aktiviert den Modus, in welchem alle Analyseresultate in einer Datei gespeichert werden. So können früher berechnete Resultate verglichen werden, ohne die Studie neu ausführen zu müssen. Bitte beachten sie, dass der Speichervorgang aller Resultate die Ausgabedatei um ca. 4.5 bis 5Mbyte pro hunderttausend Freiheitsgrade vergrößert.
Unter [Nichtlinearität] können Sie eine Analyse mit dem Einbezug von großen Verschiebungen durchführen.
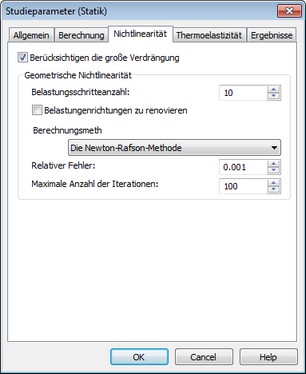
In der Anwendung gibt es Situationen in welchen die Verschiebung an gewissen Punkten sehr wichtig sind, beispielsweise in der Luft- oder Raumfahrt, oder im Design von Radio-Teleskopen, Kühltürmen oder dünnwändigen Strukturen. in solchen Fällen sollten die nonlinearen Effekte berücksichtigt werden, weil die Annahmen auf welchen die Lineare Analyse basiert nicht gültig sind. Die Option "Berücksichtigung von großen Verschiebungen" sollte aktiviert werden, wenn mindestens eine dieser Annahmen nicht erfüllt sind:
1. Die resultierenden Deformationen sind genug klein, sodass die Steifheitsveränderungen ignoriert werden können.
2. Bei der Anwendung der Belastungen und Restriktionen werden keine Amplituden, Richtungen oder Verteilungen verändert.
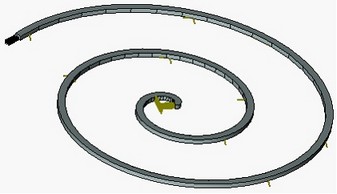
Zum Beispiel wird die lineare Analyse eines Spiralförmigen Objekts mit einer Belastung am Ende eine Fehlerquote von ca. 30% verglichen zur nichtlinearen Analyse. Dieser Unterschied der Resultate ist wegen der Annahme von kleinen Verschiebungen in der linearen Analyse.
|
|
Lineare Analyse |
Nichtlineare Analyse |
Die Kontrollen in der Gruppe «Geometrische Nonlinearität» erlauben es, den Prozess der Lösung der geometrisch nichtlinearen Problemen einzustellen.
Um diese Probleme zu lösen, organisiert ein nonlinearer Solver mit Zeitschrittverfahren den Prozess und gibt die Ergebnisse im linearisierten Gleichungssystem für jeden Schritt für die Belastungsvektoren aus.
Anzahl von Belastungsschritte. Diese Option ermöglicht es dem Nutzer die Anzahl von Schritte, während deren sich die Belastung von null zu einem bestimmten Wert verändert. Es gibt jedoch die Möglichkeit einer nicht-einzigartigen Lösung, und die gefundene Lösung könnte keinen Physikalischen Sinn ergeben. In diesen Fällen ist es sinnvoll die Belastungen schrittweise anzugeben und eine nichtlineare Lösung für jeden Schritt zu berechnen. Aus einem rechnerischen Sichtpunkt ist dies oft effizient, weil die nonlinearen Effekte kleiner werden mit jedem Schritt. Wenn die Schritte genügend klein sind, kann jede einzelne Lösung in einem Schritt mit einer hohen Genauigkeit gefunden werden. Standardmäßig ist die Anzahl Schritte auf 10 eingestellt.
Aktualisierung der Lastrichtung. Dies erlaubt es dem Nutzer Veränderungen des Lastvektors entsprechend der defomierten Geometrie des Modells in Betracht zu ziehen.
Lösungsmethode. Standardmäßig wird die Newton-Raphson Methode verwendet. Bei jedem Schritt der Lastanwendung werden die algebraischen Gleichungen bis zu einem relativen Fehler zwischen zwei aufeinanderfolgende Lösungen größer ist als die angegebene Toleranz. Wenn die Anzahl der Iterationen einen größeren Wert als die Angegebenen werden die Berechnungen beendet.
Anhang (Referenzen)
Eigenschaften von Strukturmaterialien
Eine richtige Zuordnung von Materialeigenschaften, die in der Struktur verwendet werden, ist eine wichtige Voraussetzung für die Korrektheit der Finite-Elemente-Analyse. Die Haupteigenschaften der Strukturmaterialien für die Statikanalyse von AutoFEM sind:
Das Elastizitätsmodul E des Materials, [N/m2] - Das ist die Rate der Spannung mit Einbezug der relativen Belastungen![]() , die sich in einem Prismaförmigen Objekt unter Achsenkräften in einem Zugtest entwickeln. In diesem Fall existiert ein einheitliches Spannungszustand in der Mitte des Objekts in der Richtung Längsrichtung. Der Wert des Elastizitätsmoduls E auf der Belastungsgrafik
, die sich in einem Prismaförmigen Objekt unter Achsenkräften in einem Zugtest entwickeln. In diesem Fall existiert ein einheitliches Spannungszustand in der Mitte des Objekts in der Richtung Längsrichtung. Der Wert des Elastizitätsmoduls E auf der Belastungsgrafik ![]() ist numerisch gleich zur Tangente des Neigungswinkels des linearen Segments:
ist numerisch gleich zur Tangente des Neigungswinkels des linearen Segments:![]() auf der Spannungsgrafik wenn ein Objekt getestet wird. Der physikalische Sinn des Modus E ist als die benötigte Spannung um die Länge des Objekts zu verdoppeln. Der Wert dieser Spannung erreicht jedoch nur selten sogar nur 1% der Kraft für die meisten soliden Objekten. Die Spannungsgrafik des getesteten Objekts hat einige Spezialpunkte die den Änderungen der Physikalischen Eigenschaften des Materials entsprechen und wird zur Evaluation der Grades an Zuverlässigkeit des Materials unter Belastungen verwendet.
auf der Spannungsgrafik wenn ein Objekt getestet wird. Der physikalische Sinn des Modus E ist als die benötigte Spannung um die Länge des Objekts zu verdoppeln. Der Wert dieser Spannung erreicht jedoch nur selten sogar nur 1% der Kraft für die meisten soliden Objekten. Die Spannungsgrafik des getesteten Objekts hat einige Spezialpunkte die den Änderungen der Physikalischen Eigenschaften des Materials entsprechen und wird zur Evaluation der Grades an Zuverlässigkeit des Materials unter Belastungen verwendet.
Elastizitätsbeschränkung σп - Die Spannung, die in oberen Schranke im Effekt einer rein elastischen Dehnung entstand.

Das Spannungs(Dilatation)-Diagramm für Kunststoffe (z.B. Kohlenstoffarmer Stahl)
Dehngrenze σТ. Eine weitere Dehnung des Objekts geschieht praktisch ohne zusätzliche Last. Dieses Phänomen wird "plastisches Fließen" und der horizontale Teil des Diagramms rechts des Biegepunkts "Bereich des plastischen Fließens" genannt. In vielen Materialien ist das plastische Fließen weniger gut sichtbar als in Kohlenstoffarmen Stählen.
Die bedingte Dehngrenze σ s wird für solche Materialien eingeführt; Das ist die Spannung entsprechend der Rest-(Kunststoff) Belastung s%. Normalerweise ist s=0.2%. Die Dehngrenze für Kunststoffe wird als Festigkeitskriterium gewählt: die maximale sichere Spannung [sy]. Erreichen Belastungen die Dehngrenze entstehen irreversible Schäden in der Struktur und sind deshalb um jeden Preis zu vermeiden. Die ultimative Festigkeit sr (rheologischer Widerstand) ist die Spannung, bei deren Überschreitung das Material bricht. Bei einer Zunahme der Belastungen gibt es einen Zeitpunkt, nach welchem auch ohne weiter Zunahme (oder sogar einer Abnahme) der Last die Spannung des Materials bis zum Bruch weiter zunimmt. Die Poisson's Rate µ charakterisiert transverse Spannung, welche sich in einem gestreckten Objekt entwickelt. In der Elastischen Zone die Spannung in der transversen Richtung ist ![]() , wo ε - die Belastung in der Längsrichtung, und µ— Poisson's Rate ist. Für isotropische Materialien liegt die Rate von Poisson im Bereich zwischen
, wo ε - die Belastung in der Längsrichtung, und µ— Poisson's Rate ist. Für isotropische Materialien liegt die Rate von Poisson im Bereich zwischen![]() .
.
Für verschiedene Stahl Grade, E = 195-206 GPa, µ = 0.23-0.31; für Aluminiumlegierungen, E = 69-71 GPa, µ = 0.30-0.33.
Elastische Eigenschaften einiger Materialien sind in der Tabelle dargestellt (Der Nenner zeigt die respektiven Kompressionseigenschaften).
Material |
Eigenschaft |
|
|
|
|
|
E, GPa |
σТ,MPa |
σE,,MPa |
δ, % |
ψ, % |
Steel ST.3 |
200 |
240/240 |
450/- |
26 |
50 |
Steel 15 |
200 |
210/210 |
350/- |
28 |
55 |
Steel 45 |
200 |
340/340 |
610/- |
24 |
45 |
Steel 30HGSA |
200 |
950/950 |
1200/- |
13 |
- |
Cast iron S-Ch-15-32 |
150 |
- |
150/640 |
0,6 |
45 |
Copper wire |
110 |
250/250 |
320/- |
15 |
- |
Duralumin D16 |
75 |
240/240 |
420/- |
18 |
- |
Delta wood (plywood) |
20 |
- |
250/160 |
- |
- |
Textolite |
30 |
75/115 |
127/168 |
1,5 |
- |
Die plastischen Eigenschaften eines Materials sind die relative Dehnung und Kontraktion beim Bruch:
![]() ,
, ![]()
wobei l0, F0 - die Länge der funktionierenden Teile des Objekts und der Bereich des Querschnitts vor Belastung ist.
lk - die Länge der funktionierenden Teile des Objekts nach dem Bruch ist
Fk - der finale Bereich des Querschnitts nach dem Bruch ist.
Die plastischen und spröden Materialszustände werden durch die relative Dehnung beim Bruch unterschieden.
Materialien, die einen genügend grossen Wert ![]() am Bruchpunkt aufweisen werden plastische Materialien genannt. Die Materialien, die spröde genannt werden ,haben einen relative Dehnung von
am Bruchpunkt aufweisen werden plastische Materialien genannt. Die Materialien, die spröde genannt werden ,haben einen relative Dehnung von ![]() .
.
Für plastische Materialien, die zur Grenze des Bruchs komprimiert werden, ist die Funktion ![]() die Gleiche wie im Falle einer Zugbelastung. Für einige plastische Materialien ist es unmöglich die Spannung analog zum rheologischen Widerstand zu finden wegen des Verflachens.
die Gleiche wie im Falle einer Zugbelastung. Für einige plastische Materialien ist es unmöglich die Spannung analog zum rheologischen Widerstand zu finden wegen des Verflachens.
Brüchige Materialien haben eine viel bessere Fähigkeit Druck zu widerstehen als Dilatationsbelastungen. Für diejenigen übersteigt die Bruch-kompressionsbelastung die Bruchkraft um ein Vielfaches. Der Bruch von spröden Materialien unter Kompression entsteht durch Rissbildung.
Spannungs-und Deformationszustand an einem Punkt
Der deformierte Zustand an einem Punkt eines deformierbaren Körpers ist mit dem symmetrischen Dehnungstensor beschrieben:
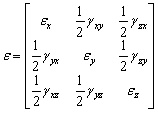 ,
,
wobei ![]() - die relative Belastung in Längsrichtung, und
- die relative Belastung in Längsrichtung, und
![]() ,
, ![]() ,
, ![]() - die Winkelbelastung ist.
- die Winkelbelastung ist.
Sie können die drei orthogonalen Richtungen immer bestimmen, damit die Scherwinkel alle Null sind, während Dehnungen ![]() sind. Die Belastungen
sind. Die Belastungen ![]() ,
, ![]() ,
, ![]() in den Richtungen, in welchem keine Scherwinkel vorhanden sind werden Hauptverzerrung an einem gewissen Punkt genannt. Zusammen ergeben die neun Belastungskomponente (drei für jede der Senkrechten Oberflächen) den sogenannten Dehnungstensor.
in den Richtungen, in welchem keine Scherwinkel vorhanden sind werden Hauptverzerrung an einem gewissen Punkt genannt. Zusammen ergeben die neun Belastungskomponente (drei für jede der Senkrechten Oberflächen) den sogenannten Dehnungstensor.
Der Tensor ist durch eine symmetrische Matrix dargestellt:
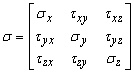 ,
,
wobei ![]() - die Zug-Druck-Belastung ist,
- die Zug-Druck-Belastung ist,
![]() ,
, ![]() ,
,![]() , - die Scherung.
, - die Scherung.

Die Spannungstensor-Komponente in einem infinitesimalen Block
Die folgende Regel wird üblicherweise für Spannungstensor-Komponente verwendet: Eine Komponente ist positiv, wenn sie in die positive Richtung der entsprechenden Achse zeigt mit einer positiven externen Normalen ausgerichtet mit einer der Koordinaten.
Der Spannungstensor und der Dehnungstensor besitzen die symmetrischen Eigenschaften ![]() ,
, ![]() ,
,![]() . Die Symmetriebedingungen des Spannungstensors werden ebenfalls gepaarte Scherungsbedingungen genannt. Die Scherung wirkt auf zwei senkrechten Flächen in den Richtungen orthogonal zu den Ecken im Schnittpunkt dieser Flächen, welche gleich der Magnitude. Wegen dieser Eigenschaften, von neun Komponenten des Spannungstensors sind sechs unabhängig. Wie im Falle der Belastung, gilt das Konzept der Hauptspannungen in einem Spannungszustand,
. Die Symmetriebedingungen des Spannungstensors werden ebenfalls gepaarte Scherungsbedingungen genannt. Die Scherung wirkt auf zwei senkrechten Flächen in den Richtungen orthogonal zu den Ecken im Schnittpunkt dieser Flächen, welche gleich der Magnitude. Wegen dieser Eigenschaften, von neun Komponenten des Spannungstensors sind sechs unabhängig. Wie im Falle der Belastung, gilt das Konzept der Hauptspannungen in einem Spannungszustand, ![]() , entsprechend der Hauptdehnung, im Zusammenhang mit dem Spannungstensor-Komponenten mit dieser Gleichung
, entsprechend der Hauptdehnung, im Zusammenhang mit dem Spannungstensor-Komponenten mit dieser Gleichung
![]() , wobei
, wobei
![]() ,
,
 ,
,

Die Lösung einer kubischen Gleichung hat drei echte Wurzeln: ![]() , welche üblicherweise folgendermaßen geordnet sind:
, welche üblicherweise folgendermaßen geordnet sind: ![]() . Die Hauptspannungen besitzen eine wichtige Eigenschaft: Die Normalspannung auf den richtungsorientierten Hauptflächen sind die höchsten verglichen zu denen auf allen anderen Flächen. Ebenfalls wird das Konzept der Mittelspannung mit folgender Formel eingeführt:
. Die Hauptspannungen besitzen eine wichtige Eigenschaft: Die Normalspannung auf den richtungsorientierten Hauptflächen sind die höchsten verglichen zu denen auf allen anderen Flächen. Ebenfalls wird das Konzept der Mittelspannung mit folgender Formel eingeführt:
![]()
Beurteilung der statischen Festigkeit einer Struktur. Festigkeitstheorie
Der ultimative Sicherheitszustand ist wenn die Materialeigenschaften qualitative Veränderungen durchmachen - eine Transition eines mechanischen Zustandes in einen anderen. Für plastische Materialien, ist der sichere Spannungszustand der Zustand der Entwicklung bemerkbarer Restspannung, während für Spröde die Situation, wenn das Material zu brechen beginnt. Dies ist nicht zulässig für Materialien. Aus diesem Grund, wenn eine Festigkeitsanalyse durchgeführt wird, muss dem zulässigen Zustand nachgegangen werden. Es entspricht der Belastung resultierend aus der Division der Belastung des höchsten Festigkeitszustandes durch einen Sicherheitsfaktor. Ist der Sicherheitsfaktor gleich in beiden Situationen, dann sind sie gleichermaßen Ausfallsicher. Um die verschiedenen belasteten Zustände zu vergleichen, wird ein einfacher Druck (Kompression) als universelle Maßnahme mit der Hauptspannung ![]() benutzt.
benutzt.
Vergleichsspannung ![]() - Die Spannung, die sich in einem gestreckten Objekt entwickelt, um deren Zustand gleich unsicher zu machen wie ein vorgegebener Spannungszustand. Das Festigkeitskriterium wird als
- Die Spannung, die sich in einem gestreckten Objekt entwickelt, um deren Zustand gleich unsicher zu machen wie ein vorgegebener Spannungszustand. Das Festigkeitskriterium wird als ![]() beschrieben. Festigkeitstheorien sind Hypothesen über Kriterien, welche die Zustände eines Materials der den ultimativen Festigkeitszustand erreicht.
beschrieben. Festigkeitstheorien sind Hypothesen über Kriterien, welche die Zustände eines Materials der den ultimativen Festigkeitszustand erreicht.
Erste Festigkeitstheorie
In der ersten Festigkeitstheorie, wird die ultimative Festigkeit als maximale Normalspannung betrachtet. Nach dieser Theorie, entsteht der instabile Zustand, wenn eine der Hauptspannungen die Sicherheitsschwelle erreicht. Entsprechend ist die Magnitude der Maximalspannung beschränkt, damit die maximale Hauptspannung ![]() nicht überschritten wird. Das Festigkeitskriterium erscheint als:
nicht überschritten wird. Das Festigkeitskriterium erscheint als: ![]() , wobei
, wobei ![]() , wenn
, wenn ![]() und
und ![]() , wenn
, wenn ![]() .
.
Zweite Festigkeitstheorie
Die zweite Festigkeitstheorie benutzt die Maximalspannung als ultimatives Festigkeitskriterium. Nach dieser Theorie ist der unsichere Zustand eines Materials erreicht, wenn die lineare Spannung eine gewisse Sicherheitsschwelle erreicht.
Für ein plastisches Material ist das Festigkeitskriterium folgend: ![]() , wobei
, wobei ![]() . Wenn, zum Beispiel
. Wenn, zum Beispiel ![]() , dann
, dann ![]() .
.
Für sprödes Material, ist das Festigkeitskriterium folgend:
![]() ,
, ![]()
Die erste Theorie liefert eine gute Übereinstimmung mit experimentellen Daten nur für spröde Materialien. Die Zweite wurde heutzutage praktisch aufgegeben.
Dritte Festigkeitstheorie
In der dritten Festigkeitstheorie ist die ultimative Festigkeit die maximale Scherung. In dieser Theorie, ist der unsichere Zustand erreicht, wenn die maximale Scherung eine gewisse Sicherheitsschwelle erreicht.
Das Festigkeitskriterium ist folgend: ![]() , wobei
, wobei ![]() .
.
Folglich: ![]()
Vierte (Energie) Festigkeitstheorie
Die vierte Festigkeitstheorie basiert auf einem Energieansatz. Basierend auf der Hypothese, dass der Grund eines unsicheren Zustandes die Magnitude der potentiellen Dichte der Deformationsenergie uф, folglich bezieht sich das Kriterium auf die Dichte der potentiellen Deformationsenergie. Die Formel für die Energiedichte wird von der Verzerrung der Formel for die vollständige potentielle Energiedichte durch Spannung anhand der spezifischen Poisson Rate von µ =0.5. abgeleitet.
Dies ergibt:
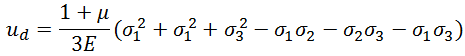
Das Festigkeitskriterium erscheint als![]() , wobei
, wobei 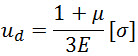 .
.
Folglich:

oder
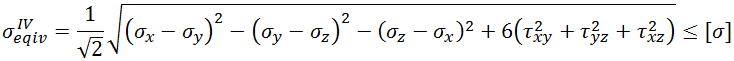
Die dritte und vierte Festigkeitstheorie produzieren eine gute Übereinstimmung der theoretischen Berechnungen mit den experimentellen Daten für plastische Materialien und werden oft für die Festigkeitsanalyse benutzt. Diese Theorien sind jedoch nicht für sprödes Material geeignet.