 |
AutoFEM Analysis Ermüdungsanalyse | ||||||
Ermüdungsanalyse
Einige Teile von Maschinen, Mechanismen oder architektonischen Strukturen sind von Belastungen getroffen, die in der Zeit variieren. Die Ermüdungsanalyse solcher Probleme ist unterschiedlich von der statischen Analyse. Das Modul der Ermüdungsanalyse von AutoFEM Analyse dient der Untersuchung der Festigkeit von Strukturen unter Zyklischen Belastungen. Die Ermüdung ist ein Prozess einer schrittweisen Anhäufung von Schäden in einem Material unter dem Einfluß von Spannungsvariabeln, die zur Entstehung von Rissen, deren Ausbildung und möglicherweise zur Zerstörung der gesamten Struktur führt.
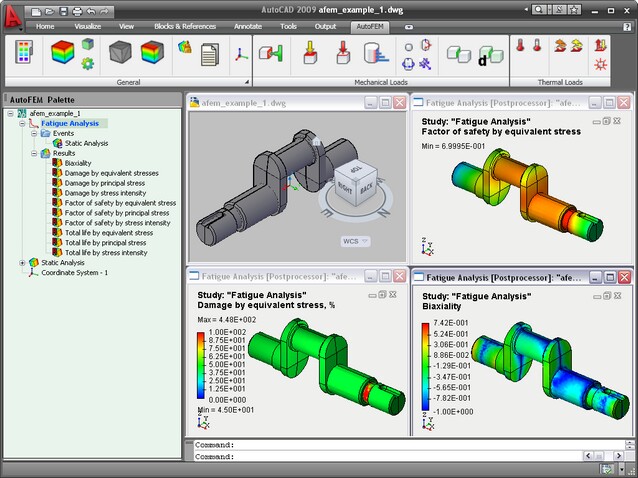
Details der Schritte der Ermüdungsanalyse
Vor der Ausführung einer Ermüdungsanalyse, müssen Sie die Effekte einer statischen Belastung auf das gegebene Objekt untersuchen. (eine Statik Analyse durchführen) Dies ist nötig, um zu wissen, ob der Ausfall des Objekts schon bei einer statischen Belastung stattfindet. Wird das Objekt schon mit einer statischen Belastung (Sicherheitsfaktor kleiner als 1), dann muss auch keine Ermüdungsanalyse durchgeführt werden. Die vorherige statische Analyse ist auch nötig, weil die Daten der gelösten statischen Belastungen (Grund- und Vergleichsspannung) für die Ermüdungsanalyse für die Berechnung der Festigkeit unter zyklischen Belastungen benötigt werden. Zusätzlich ist es für die Ermüdungsanalyse nötig die S-N Kurve zu bestimmen für das Material, aus welchem das Objekt hergestellt wurde.
Eine Ermüdungsanalyse erstellen
Sie können eine der folgenden Möglichkeiten benutzen, um eine Studie zu erstellen:
Kommando: |
_FEMASTUDY |
Hauptmenü: |
AutoFEM | Studie erstellen... |
Symbol: |
|
Sie müssen den Typ der Studie ("Ermüdung") im Eigenschaftsfenster angeben.
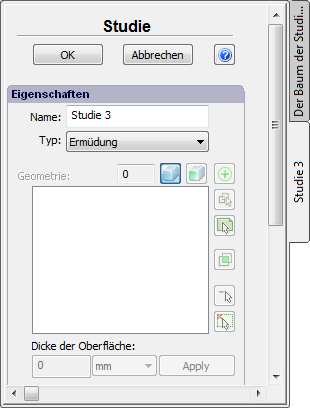
Um eine zyklische Belastung zu kreieren müssen Sie folgende Schritte ausführen:
Öffnen Sie das Eigenschaftsfenster des Ermüdungszyklus, indem Sie in der Gruppe "Ereignisse" in der "AutoFEM Palette" mit einem Rechtsklick![]() aufrufen, dann den Befehl "Ereignis hinzufügen.." aus dem Kontextmenü auswählen.
aufrufen, dann den Befehl "Ereignis hinzufügen.." aus dem Kontextmenü auswählen.
Fügen Sie die schon berechnete statische Studie hinzu;
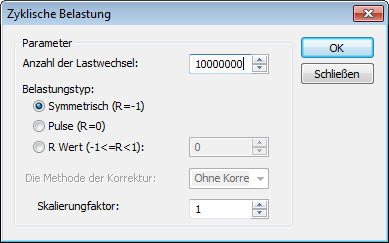
Wählen Sie die Parameter der Ermüdungszyklen : Anzahl der Lastwechsel, Belastungstyp und Skalierungsfaktor.
Es ist möglich, eine Ermüdungsanalyse für mehrere Ereignisse aus verschiedenen statischen Analysen durchzuführen. Zum Beispiel, wenn zwei oder mehr Kräfte zyklisch sind, aber verschiedene Gesetze der Variation haben. Beachten Sie, dass die Finite-Elemente-Netze der statischen Studien identisch sein müssen, und der Körper jeder Studie das selbe Material haben muss.
Es kann auch der "Faktor der Belastungskonzentration" (standardmäßig 1) unter [Ermüdung] in den Studieneigenschaften eingestellt werden.
Die Resultate der Ermüdungsanalyse
Nach der Berechnung wird ein neuer Ordner ("Resultate") im Studienbaum erstellt. Sie können die Liste der angezeigten Resultate unter [Resultate] in den Studieneigenschaften bestimmen.
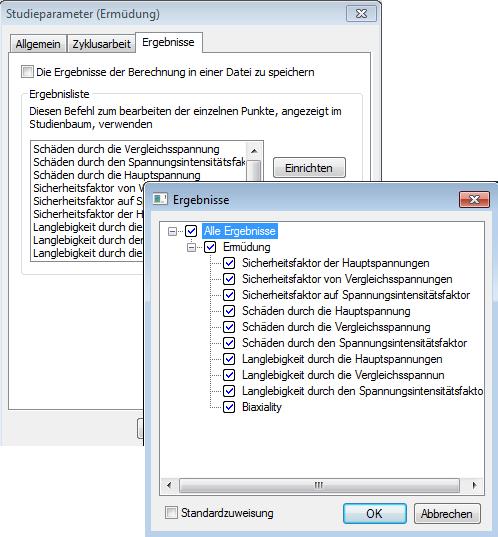
Insgesamt 10 Ergebnisse sind in der Ermüdungsanalyse verfügbar. Sie können in vier Gruppen eingeteilt werden.
Die Gruppe "Beschädigung" enthält die folgenden Ergebnisse:
• Beschädigung durch Grundspannungen;
• Beschädigung durch Vergleichsspannungen;
• Beschädigung durch Spannungskraft;
Das Ergebnis wird in Prozent dargestellt und zeigt den Schädigungsgrad der Struktur unter dem Einfluß von zyklischen Belastungen mit dem bestimmten Anzahl und Art der Zyklen.
Ist das Objekt Subjekt von n1 Zyklen von Vergleichsspannung S1, n2 Zyklen von Vergleichsspannung S2, n3 Zyklen von Vergleichsspannung S3, ..., nk Zyklen von Vergleichsspannung Sk, dann ist die gesamte Schadensrate D wie folgt berechnet:
D = n1 / N1 + n2/N2 + n3/N3+...+ nk/Nk , wobei Ni die Anzahl Zyklen ist die den Ausfall des Objekts auslösen, mit Si.
Die Gruppe "Lebensdauer" (Dieser Typ von Resultaten ist nur für Studien mit einem einzelnen Ereignis verfügbar) enthält die folgenden Ergebnisse:
| • | Lebensdauer bei Grundspannungen; |
| • | Lebensdauer Vergleichsspannungen; |
| • | Lebensdauer bei Spannungskraft. |
Dieses Resultat zeigt die Mindestanzahl an Zyklen Nmin, welche zum Ermüdungsausfall führen können.
Die Gruppe "Sicherheitsfaktor" (Dieser Typ von Resultaten ist nur für Studien mit einem einzelnen Ereignis verfügbar) enthält die folgenden Ergebnisse:
| • | Sicherheitsfaktor bei den maximalen Grundspannungen. (Hypothese 3) |
| • | Sicherheitsfaktor bei Vergleichsspannungen (Hypothese 2) |
| • | Sicherheitsfaktor bei Spannungskraft (Hypothese 1) |
Der Sicherheitsfaktor ist die Rate der Ermüdungsgrenze σR, definiert für eine gegebene Ermüdungskkurve und eine gegebene Anzahl Zyklen und der Amplitude der Zyklen σ*, welche aus den Berechnungen der statischen Analyse stammen. σ: ![]()
Die Belastungen σ werden auf der Basis der relevanten Plastizitätsbedingungen berechnet:
| • | Die Hypothese der Energieverzerrung |
| • | Die Hypothese der maximalen Scherung. |
| • | Die Hypothese der größten Hauptspannung: |
Die Gruppe "Zweiachsigkeit". (Dieser Typ von Resultaten ist nur für Studien mit einem einzelnen Ereignis verfügbar) enthält die folgenden Ergebnisse:
Zweiachsigkeit ist das Verhältnis der kleineren abwechselnden Grundspannung (nicht Null), zur größeren abwechselnden Grundspannung:
![]() .
.
Dieses Resultat charakterisiert die Ungleichheit der Amplituden der Hauptspannung in einem Punkt und beschreibt die räumliche Verteilung der Ungleichmäßigkeit der Hauptspannung auf dem Volumen eines Körpers an jedem Punkt. Der Wert der Zweiachsigkeit gleich 1 entspricht dem Fall von gleichen Belastungszuständen σ1=σ2=σ3 an diesem Punkt.
Anhang (Referenzen)
Der Belastungszyklus. Die generellen Eigenschaften
Nach einer bestimmten Anzahl von Belastungszyklen kann die Zerstörung eines Objekts stattfinden. Es ist jedoch auch möglich, dass die Zerstörung dieses Objekts bei konstanter (statischer) Belastung nicht stattfindet. Die Anzahl der Zyklen vor dem Ausfall ist abhängig von der Amplitude der Belastung und kann eine große Variation beinhalten. Mit grossen Belastungen können 5-10 Zyklen ausreichen, um das Objekt zu zerstören, unter kleinen Belastungen können es Millionen oder Billionen Zyklen sein, oder gar unendlich viele. Die maximalen σmax und minimalen σmin Belastungszyklen helfen bei der Berechnung des algebraischen Werts. Mit der Mittelbelastung σm und Amplitude σa ist der Belastungszyklus folgender:
σm= ( σmax + σmin ) / 2 , σa= ( σmax - σmin ) / 2. Die Größe der Belastung ist der Unterschied zwischen dem Maximum und dem Minimum des Belastungszyklus: z.B. 2σa= ( σmax - σmin ).
Der Zyklus bei welchem der maximal- und Minimalwert in absoluten Werten verschieden ist, wird asymmetrisch genannt. Ein Spezialfall des asymmetrischen Zyklus ist der pulsierende Zyklus bei welchem der Minimum Belastungszyklus Null ist: σmin = 0.
Ein Symmetrischer Zyklus ist einer in welchem die Maximal und Minimalbelastung gleich der Amplitude sind, aber mit negativem Vorzeichen. Um den Grad der Asymmetrie zu charakterisieren wir die Belastungsasymmetrierate benutzt, welche die Rate des minimalen zum maximalen Belastungszyklus ist:
R=σmin/σmax .
Art des Belastungszyklus : |
Asymmetrisch |
Pulsierend |
Symmetrisch |
Belastungsrate R=σmin/σmax : |
R1 |
0 |
-1 |
Minimalbelastung σmin : |
R1*σmax |
0 |
- σmax |
Maximalbelastung σmax : |
σmax |
σmax |
σmax |
Mittelspannung σm : |
(1 + R1 )*σmax/2 |
σmax/2 |
0 |
Belastungsbereich σa : |
(1 - R1 )*σmax/2 |
σmax/2 |
σmax |
Belastungsbereich 2σa : |
(1 - R1 )*σmax |
σmax/2 |
2*σmax |
|
|
|
||
Asymmetrischer Zyklus ( R= - 0.2) |
Symmetrischer Zyklus ( R= -1 ) |
Pulsierender Zyklus ( R= 0 ) |
Methoden der Belastungskorrektur
Lassen wir σ* die korrigierte Wechselbelastung sein, σY ist die Fliessspannung, σT ist die Zugfestigkeit, dann:
| 1. | Soderberg Methode σ* = σa / ( 1 - σm / σY ) |
| 2. | Goodman Methode für spröde Materialien σ* = σa / ( 1 - σm / σT ) |
| 3. | Gerber Methode für plastische Materialien σ* = σa / ( 1 - ( σm / σT )2 ) |
Evaluation der Charakteristiken des Ermüdungswiderstandes in einem komplexen Belastungszustand
Festigkeitsbedingungen mit wechselnden Belastungen ist generell ähnlich zu Festigkeitsbedingungen einer statischen Analyse, aber die maximal erlaubte Belastung ist die Ermüdungslimite σR . Ensprechend nimmt die Hypothese die Ermüdungsfestigkeitskriterien testet in der Ermüdungsberechnung die Form σ* ≤ σR. Wir erinnern an die generellen Ausdrücke der traditionellen Hypothesentests der Festigkeit (für Plastizitätsbedingungen), die für Festigkeitsberechnungen genutzt werden:
| 1. | Tresca - Saint-Venant Hypothese ( Die Hypothese der maximalen Scherung) σY < ( σ1 - σ3 ), | σ1 | ≥ | σ2 | ≥ | σ3 | |
| 2. | Huber - Mises Hypothese (Hypothese der Energieverzerrung) |
| 3. | Mohr Hypothese (Hypothese der größten Hauptspannung) σY < σ1 , | σ1 | ≥ | σ2 | ≥ | σ3 | |
wobei σY Fliessspannung ist, σ1 , σ2 , σ3 und die Hauptspannungen. Folglich, wenn die Ermüdungen analysiert werden, resultieren drei Optionen für den Sicherheitsfaktor entsprechend jeder der generell akzeptierten Theorien der Festigkeit.