Forzado Oscilaciones armónicas

Forzado oscilaciones armónicas

Análisis de oscilaciones forzadas se realiza para predecir el comportamiento de una estructura bajo las acciones exteriores que cambian de acuerdo con la ley armónica. Estas acciones incluyen la fuerza y / o excitación cinemática. Además de ello, el impacto de la amortiguación del sistema puede ser tomada en cuenta.

El objetivo del análisis de oscilación forzada es obtener una dependencia de la respuesta del sistema en frecuencia de las acciones de peso. Como resultado de los cálculos obtenemos amplitudes de los desplazamientos, aceleración de la vibración, y la sobrecarga de la vibración a la frecuencia de peso preestablecido. De acuerdo con estos resultados, se puede obtener, para una gama de frecuencias, las amplitudes y las dependencias de aceleración de la vibración en la frecuencia de las acciones de peso, lo cual es importante con la evaluación de la estabilidad de la vibración del sistema en este rango de frecuencia predeterminada.

Introducción.

El módulo "Oscilaciones forzadas" del sistema de modelado de elementos finitos, Análisis AutoFEM, se pueden utilizar para el análisis de las oscilaciones forzadas establecidas de los siguientes tipos:

•

Forzado oscilaciones del sistema sin cuenta de amortiguación bajo la acción de la fuerza convincente armónica. En el sistema con numerosos grados de libertad, estas oscilaciones se describen mediante el siguiente sistema de ecuaciones diferenciales lineales:

,
donde M es una matriz cuadrada simétrica de la masa;

K es una matriz de rigidez cuadrada simétrica del sistema;

F0 es un vector de amplitudes de obligar a la acción;

w es la frecuencia de la acción convincente;

u, u'' son los vectores de coordenadas de los puntos del sistema, que cambian su posición en el tiempo t, y sus aceleraciones;

j es la fase inicial de la excitador.

•	Forzado oscilaciones del sistema con la cuenta de amortiguación bajo la acción de la fuerza convincente de armónicos. Estas oscilaciones se describen mediante el siguiente sistema de ecuaciones diferenciales lineales: ,

•

Donde C es la matriz cuadrada simétrica de amortiguación y u' es vector de la velocidad de los puntos del sistema. Suponemos que el sistema se amortigua de conformidad con la ley de Rayleigh, es decir, es proporcional a la distribución de rigideces y masas del sistema y se define con la ecuación

donde A es una relación de aspecto de masas y b es una relación de aspecto de la rigidez (ambas relaciones son escalares).

•

Oscilaciones forzadas del sistema de los dos tipos anteriores, derivados de los desplazamientos de los apoyos bajo la ley armónica, es decir, con lo que se producen un sistema de apoyos para el desplazamiento oscilatorio. Ecuaciones diferenciales que describen este tipo de oscilaciones son análogos a los establecidos anteriormente, pero difieren en la fuerza convincente de armónicos que se calcula a través de la fórmula:

Varias fuerzas y / o desplazamientos de peso de los soportes se pueden aplicar al sistema, pero sus frecuencias deben ser iguales.

La rotación de un eje o husillo en el estado de desequilibrio en soportes elásticos puede servir un ejemplo de la fuerza convincente armónica. Cinemática de excitación se aplica cuando no se conocen los valores de las fuerzas de peso, en contraste con amplitudes de oscilaciones de algunos elementos de la estructura que se conocen.

Al considerar las oscilaciones forzadas, es importante tener en cuenta el impacto de las fuerzas de amortiguación. El proceso de disipación de energía de las oscilaciones mecánicas, lo que lleva al paso a paso atenuación de sumas globales oscilaciones producidas del sistema, que se denomina " de amortiguación ". Fuerzas de amortiguación pueden tener diferente origen, a saber: la fricción entre sus caras deslizamiento en seco, la fricción entre sus caras lubricabas, la fricción interna, aire o resistencia a los líquidos, etc Por lo general se supone que la fuerza de amortiguación es proporcional a la velocidad ( amortiguamiento viscoso ). Fuerzas de la Resistencia cambiantes en virtud de la ley voluntaria se sustituyen por fuerzas de amortiguación equivalentes, partiendo de la condición de que en un ciclo, que disipan la misma cantidad de energía en forma de fuerzas reales. La ecuación para oscilaciones forzadas con la cuenta de amortiguación para la i-ésima de masa, que es la solución de las ecuaciones diferenciales anteriores, se da a continuación:
,
Donde ω0 es la frecuencia angular de la amortiguación, w es la frecuencia angular de la fuerza convincente.
2n=c/m ,
Donde ci es el factor de amortiguamiento para i th modo, y mi es la masa. Se compone de dos términos: la expresión en paréntesis describe atenuar las oscilaciones libres en la frecuencia de amortiguación que se diferencia poco de la frecuencia de las oscilaciones libres, y el resto corresponde a oscilaciones forzadas con la frecuencia de la acción w forzada.

Con el fin de aclarar el impacto de amortiguación, consideremos la figura que presenta el gráfico de la dependencia del factor de ganancia de las amplitudes

En la relación de frecuencias de las oscilaciones forzadas y gratuitas w/w0 a diferentes valores del factor de amortiguamiento γ=n/ω=c/ccritical, Donde ccritical es factor crítico de amortiguamiento viscoso, en el que las oscilaciones no se producen mientras que el desplazamiento del sistema decae monótonamente.

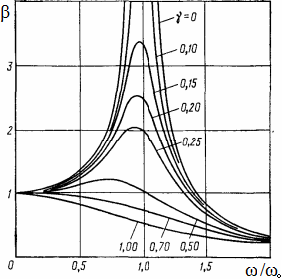
La figura muestra que, cuando la frecuencia de oscilaciones forzadas es baja en comparación con la propia frecuencia de las oscilaciones libres, el desplazamiento de los puntos del sistema es aproximadamente igual al desplazamiento en carga estática, impulsado por la fuerza convincente. Cuando la fuerza armónica de conducción tiene una alta frecuencia, independientemente de que el factor de amortiguamiento, no causar oscilaciones forzadas del sistema, que tiene una baja frecuencia propia. En ambos casos ω<<ω0 and ω>>ω0, de amortiguación no afecta prácticamente las oscilaciones forzadas, aunque cuando la relación de las frecuencias por encima es de aproximadamente 1, de amortiguación plantea un impacto significativo en el factor de ganancia. Al pequeño factor de amortiguación, el mayor impacto de la amortiguación se observa cerca de las frecuencias de resonancia, que es crucial tener en cuenta en el análisis de las estructuras. Para los propósitos de análisis de oscilaciones forzadas de una estructura cerca de las frecuencias propias, se proporciona la importación de los valores de las frecuencias propias de los resultados de cálculo de la análisis de frecuencia (ver más abajo).

Amortiguación gj factor para la j-ésima modalidad está vinculada a las relaciones de aspecto a, b por la ecuación
.

El valor del factor g de amortiguación toma valores de 0,01 para los sistemas débilmente amortiguadas (partes todas de metal); 0,02-0,04 (estructuras metálicas con uniones permanentes, que se deforman por debajo de la resistencia a la fluencia); 0,03-0,07 (estructuras de metal con en-cortar las conexiones); 0,05 para el caucho, y hasta 0,15 para los sistemas fuertemente amortiguadas.

Si se conocen los factores de amortiguación para la i-ésima y j-ésima modos, que las relaciones de aspecto se calculará con arreglo a las fórmulas:
,
.
Si el coeficiente a es igual a cero, tales amortiguación se llama relativa, y el factor de amortiguamiento para el j-ésimo modo será proporcional a la frecuencia angular de ese modo sin amortiguación. Por lo tanto, las oscilaciones que corresponden a modos superiores atenuarán más rápido. Si el coeficiente b es igual a cero, tales amortiguación se denomina absoluta, y el factor de amortiguamiento para el j-ésimo modo será inversamente proporcional a la frecuencia angular de este modo sin amortiguación. Por lo tanto, las oscilaciones correspondientes a los modos más bajos atenuarán más lento.

Los principales resultados del cálculo en el módulo de oscilaciones forzadas son los siguientes valores:

•	Amplitudes de los desplazamientos en elementos finitos de malla de nodos Um;

•	Aceleraciones vibratorias en nodos de la malla de elementos finitos expresados a través de amplitudes Um as U''m=Umω2 ;

•	Sobrecargas de vibración, que se define como la relación de la aceleración de la vibración a la aceleración de caída libre U''m/g.

Etapas del análisis de las oscilaciones forzadas "

1.	Creación de "Estudio". Al crear un estudio, debe indicar su tipo, " Oscilaciones forzadas " en la ventana de propiedades de comando. Es posible crear una copia del tipo de estudio " Análisis de frecuencias " y cambie el tipo, en este caso, las condiciones de malla y de frontera serían trasladados.

2.	Ajuste de materiales. Para establecer los materiales, es necesario hacer clic en el botón derecho del ratón en el cuerpo desde la carpeta "Bodies" ( o en la carpeta en sí con el fin de establecer el mismo material para todos los cuerpos ) y seleccione la opción del "Material".

La imposición de condiciones de frontera. En el análisis de las oscilaciones forzadas, como en el análisis estático, fijaciones y cargas juegan el papel de las condiciones de frontera. En este tipo de análisis, se pueden utilizar todos los tipos de fijaciones y cargas de fuerza. La imposición de las fijaciones y la fuerza de cargas es la condición obligatoria de cálculo sea correcto. En total, las limitaciones impuestas al desplazamiento del cuerpo deberán cumplir las siguientes condiciones.

Para el análisis estático, el modelo debe tener una fijación con exclusión de sus moverse libremente en el espacio como el cuerpo sólido. El incumplimiento de esta condición daría lugar a resultados incorrectos de la modelización de elementos finitos o el fracaso del proceso de cálculo. Además, la carga cinemática " oscilador " podrá sustituir fijaciones parciales o completas.

Ajuste de las frecuencias y la amortiguación. Realización de cálculos. Antes del cálculo, el usuario deberá indicar en las propiedades del estudio los valores de las frecuencias de las acciones de carga, para lo cual se llevará a cabo el análisis de oscilaciones forzadas, así como el valor de atenuación.

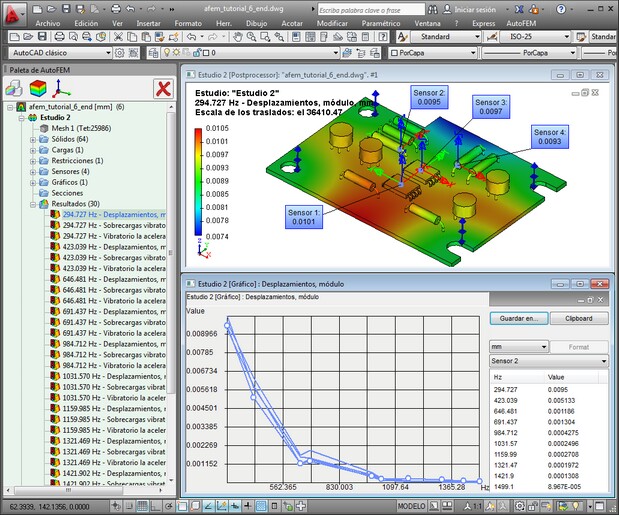
Obtención y análisis de los resultados. Para ajustar con precisión los resultados mostrados, debe hacer clic en el botón derecho del ratón en la carpeta de "resultados" en el árbol de los estudios y de selección de elementos "Resultados". Los resultados del análisis de oscilación forzada: amplitudes de los desplazamientos, aceleraciones de vibración o sobrecargas de vibración, y las fases de las oscilaciones. Para cada tipo de "resultado" se ofrece la oportunidad de ver el estado deformado de una estructura en diferentes fases.

Ajustes específicos de la instalación del preprocesador en el Análisis de Oscilación Forzada

1.	Ajuste de limitación. El modelo puede estar restringido por las limitaciones tanto completos y parciales. Cuando se establecen limitaciones parciales, se prohibe el establecimiento de desplazamientos que no sean cero.

2.	Ajuste de la fuerza de carga. Para configurar la amplitud de cargas de fuerza, los siguientes tipos de cargas se pueden aplicar a quilates, bordes o vértices de un modelo (la aceleración se puede aplicar a los órganos):

•	La fuerza;

•

Presión;

•	Aceleración;

•	Carga cilíndrica

•

De par.

Un número de cargas puede la acción del sistema de órganos de forma simultánea, pero todos ellos tienen la misma frecuencia. Para cada una de las cargas permitidas, su propia fase inicial de oscilaciones se puede ajustar.

Ajuste de la carga cinemática (oscilador). Para establecer la amplitud de oscilación del soporte, se debe aplicar la carga oscilador a elementos del modelo, que se pueden utilizar en lugar de la fijación total o parcial. La carga se aplica a los quilates, aristas o vértices de los cuerpos, así como a los órganos individuales de la asamblea. Con el fin de especificar la dirección de oscilaciones LCS está seleccionado en el comando, y la dirección en sí se indica mediante una marca de verificación, lo que corresponde al eje pertinentes LCS. El tipo de carga cinemática se selecciona de la lista desplegable y podría ser la siguiente:

•	Amplitud de los desplazamientos de punto;

•	Velocidad;

•	Aceleración;

•	Sobrecarga.

En el campo independiente, se puede configurar el cambio de fase, medida en grados o radianes.

En la combinación de la carga del oscilador y fijaciones parciales, direcciones de oscilaciones y limitaciones deben ser diferentes para un único elemento del modelo.

Configuración del procesador de análisis de las oscilaciones forzadas

En la ficha [General], es posible determinar o cambiar las propiedades descriptivas del presente estudio, es decir: nombre, tipo de estudio, y el comentario.

En la ficha [Parámetros], es posible determinar o cambiar las frecuencias de la acción exterior, parámetros de Rayleigh de amortiguación.

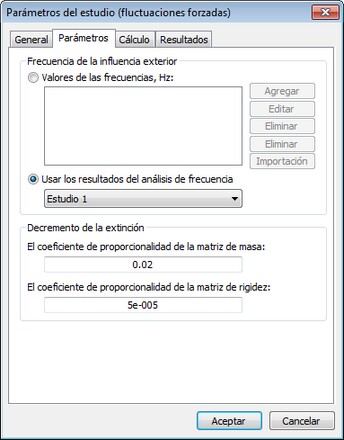
En el grupo de parámetros "Frecuencias de la acción exterior", se establecen valores de frecuencias relativas a las acciones de las cargas externas. Allí varias maneras de agregar nuevos valores:

1.	Botón [Agregar] permite la adición de tanto el valor único de la frecuencia y de una gama de frecuencias, por el que se especifican el valor inicial, valor final y la ganancia.

2.	Botón [Importar] pone de manifiesto la ventana de diálogo en la que los valores de las frecuencias de resonancia se pueden importar de resultados del análisis de frecuencia realizado anteriormente.

Cuando sea necesario para el cálculo de las oscilaciones forzadas sólo en todas las frecuencias de resonancia, determinado a través del análisis de la frecuencia anterior, debe activar el control de elemento " Use los resultados del análisis de frecuencia." En este caso, se mantiene la conexión asociativa con los resultados del análisis de frecuencia seleccionada, es decir, en el cambio de los resultados del análisis de frecuencia, los valores de los propios valores actualizados se utilizan automáticamente para el análisis de oscilación forzada.

Sobre la lista existente de valores de frecuencia, las siguientes operaciones de edición están disponibles:

•	Botón [Cambiar] permisos para volver a escribir el valor de un solo valor específico;

•	Botón [Quitar] elimina el valor de la frecuencia seleccionada de la lista;

•	Botón [Borrar] borra fuera toda la lista de valores de frecuencia.

En el grupo de parámetros "amortiguamiento de Rayleigh", se definen los valores de los factores de la estructura a y b de amortiguación.

Tabla [Resolver] permisos para establecer las propiedades del procesador para la solución de un sistema de ecuaciones. Parámetros, que definen la configuración del procesador, son similares a aquellos en el análisis estático.

Tabla [Resultados] permite determinar los tipos de resultados, que se muestran en el árbol de estudio en el cálculo.

Configuración y análisis de los resultados de oscilaciones forzadas postprocesador

En la ficha [Resultados], uno puede ver los siguientes tipos de resultados divididos en ocho grupos:

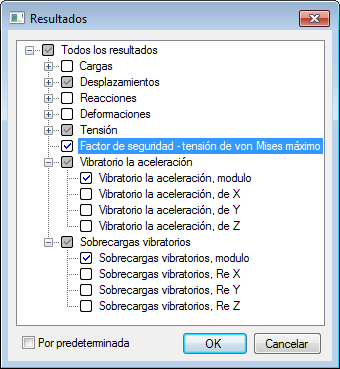
El grupo de "un montón" incluye los siguientes resultados: componentes aplicados al modelo de elementos finitos y el módulo de cargas reducidas a los nodos. Este tipo de resultados es orientativo.

Los "Desplazamientos" grupo incluye:

•	Los desplazamientos de los puntos del modelo de elemento finito con la cuenta del desplazamiento de fase relativo a la fase de excitación en la dirección de los ejes de sistema de coordenadas mundial (CS): , , , así como el desplazamiento modulo .

•	Parte real de los desplazamientos en la dirección de los ejes de CS mundial: Re(UX), Re(UY), Re(UZ), así como el módulo de la parte real de desplazamientos .

•	Parte virtual de los desplazamientos en la dirección de los ejes de mundial CS: Im(UX), Im(UY), Im(UZ), así como el módulo de la pieza virtual de desplazamientos .

•	Amplitud de los desplazamientos de los puntos del modelo de elementos finitos (sin cuenta del desplazamiento de fase relativo a la fase de excitación) en la dirección de los ejes de mundial CS: UXm, UYm, UZm, así como el módulo de amplitud .

•	Ángulos de fase para componentes de desplazamiento de puntos del modelo de elementos finitos en la dirección de los ejes de CS mundial en relación con la fase del excitador , , , así como el módulo de ángulo de fase .

En el caso si el desplazamiento de fase está preajustado, se puede obtener Epures separados para los componentes reales y virtuales de desplazamientos, así como el valor absoluto de la fase en los puntos del modelo de elementos finitos.

En el grupo de "aceleración de la vibración", uno puede notar la derivación de epures de amplitudes de las aceleraciones de vibración correspondientes a los puntos del modelo de elementos finitos U''m=Umω2 . La fase de aceleración de la vibración difiere en 180 (π rad) de la fase de desplazamiento.

En el grupo "sobrecargas de vibración", se puede observar la derivación de epures de sobrecargas de vibración U''m/g, medido con respecto a la aceleración de caída libre.

También la gráfica del resultado se puede mostrar.