Propósito y función de mallas de elementos finitos

El propósito principal de una malla de elementos finitos es a la geometría adecuada aproximada del cuerpo que está siendo modelado, que representan todas las características de la geometría de la parte significativa de la solución. El preprocesador de AutoFEM utiliza un generador eficaz automática de mallas de elementos finitos, que permite al usuario controlar varios modos de generación de la malla con el fin de obtener mallas de la calidad deseada en diferentes modelos. En Análisis AutoFEM,  volumétricos elementos finitos tetraédricos y superficiales elementos finitos triangulares se utilizan en mallas de elementos finitos, que, en teoría, permiten aproximación con cualquier precisión requerida. Sin embargo, hay varias recomendaciones preliminares acerca de la adecuación de los modelos de cálculo con elementos finitos.

En primer lugar, la calidad de una solución puede depender de la forma de los elementos finitos. Los mejores resultados de la modelización de elementos finitos se logran, si los elementos (tetraedros y triángulos) que forman el modelo de malla están cerca de los equiláteros. Esto es especialmente importante para elementos tetraédricos. Viceversa, si un modelo de malla contiene elementos, cuyos bordes varían en su tamaño en gran medida, a continuación, los resultados de la modelización podría ser de una precisión insuficiente. En tales casos, es deseable reducir al mínimo el número de tales elementos indebidas por medio de las opciones del generador de elemento finitos de malla.

Por lo tanto, un usuario tiene que controlar "calidad" del modelo de elementos finitos basada en una inspección visual o con la ayuda de « parámetros de malla », con el objetivo de distribución posiblemente más forma uniforme de los elementos que intervienen en la malla.

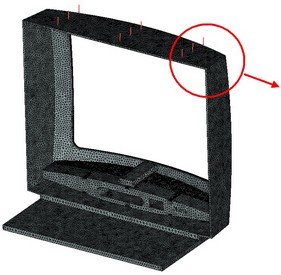
Malla más adecuada obtenido después de usar la configuración de los parámetros de malla

En segundo lugar, además de las formas de los elementos finitos, la calidad de la solución se ve directamente afectada por el grado de discretización del modelo original geométrica, que es «densidad» de la malla de elementos finitos.  El usuario puede controlar este parámetro de malla mediante la especificación de un tamaño medio absoluto o relativo de los elementos finitos, o mediante la variación de los parámetros que afectan a la generación de mallas en los modelos curvilíneos. Por lo general, una división de modelo 3D en una cantidad más grande de elementos conduce a mejores resultados en términos de precisión. Sin embargo, recuerde que se aproxima a un modelo por un gran número de pequeños elementos finitos conduce inevitablemente a un sistema de alto orden de las ecuaciones algebraicas, que podría afectar negativamente a la velocidad de los cálculos.Calidad de un modelo de elementos finitos puede evaluarse posteriormente por resolver varios estudios con creciente grado de discretización. Si la solución (como máximos desplazamientos y tensiones) ya no muestra diferencias significativas en una malla más densa, pues, a una gran certeza, se puede considerar como un nivel de discretización óptima, de modo que una mayor tasa de discretización es injustificada.

En muchos casos, se puede considerar el nivel mínimo de división de un cuerpo como que la entrega de dos a tres capas de elementos finitos en la dirección de la aplicación de cargas y desplazamientos esperados.

Además, el generador de mallas proporciona medios para la creación de usuario-impuesta malla «refinamiento» en las áreas del modelo con variaciones bruscas en la curvatura, donde uno esperara altos gradientes de los valores buscados (tensiones, por ejemplo).

Por lo tanto, se debe prestar mucha atención al modelo de malla que se generan para un modelo de elementos finitos, viendo que la malla de elementos finitos corresponde a la geometría del modelo y tenía una calidad satisfactoria desde el punto de vista de una solución fiable y de confianza para el problema físico que se está modelando.