Analyse d'Oscillations harmoniques forcées

L'analyse des oscillations forcées est effectuée pour prédire le comportement d'une structure sous des actions extérieures qui changent conformément à la loi harmonique. Ces actions comprennent la force et/ou l'excitation cinématique. En plus de cela, l'impact de l'amortissement du système peut être pris en compte.
L'objectif de l'analyse des oscillations forcées est d'obtenir une dépendance de la réponse du système à la fréquence des actions immédiates. À la suite des calculs, nous obtenons les amplitudes des déplacements, une accélération de la vibration et la surcharge de vibrations à la fréquence prédéfinie.Selon ces résultats, nous pouvons obtenir, pour une gamme de fréquence, les dépendances des amplitudes de vibration et d'accélération de la fréquence, ce qui est important à l'évaluation de la stabilité des vibrations du système dans cette gamme de fréquence prédéfinie.

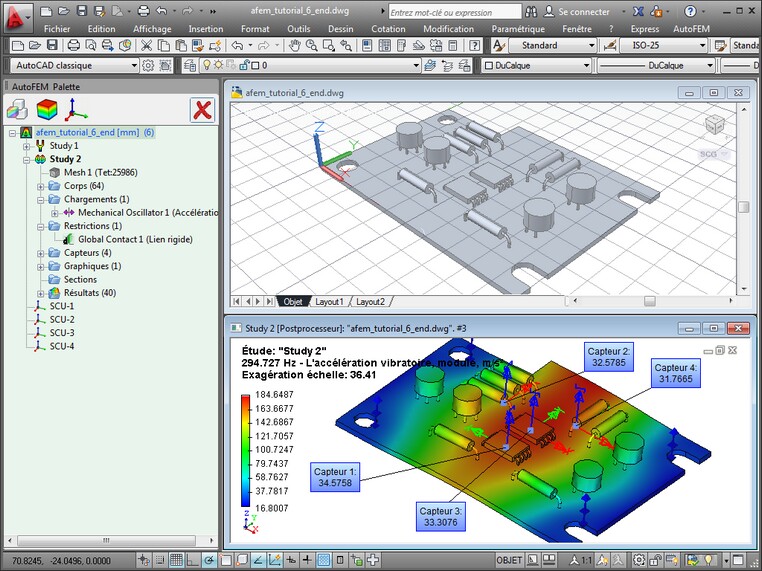
Introduction

Le module "Oscillations forcées" du système de modélisation d'éléments finis de AutoFEM peut être utilisé pour analyser les oscillations forcées établies des types suivants:

•	Des oscillations forcés du système avec aucun amortissement sous l'action de la force d'attraction harmonique. Dans un système avec de nombreux degrés de liberté, ces oscillations sont décrites par le système d'équations différentielles linéaires suivant:

ou M est une matrice carrée symétrique de masse;
K est une matrice carrée symétrique de rigidité du système;
F0 est un vecteur des amplitudes d'action convaincante;
ω est la fréquence de l'effet irrésistible;
u, u'' sont des vecteurs de coordonnées des points du système qui changent leur position au temps t, et leurs accélérations;
φ est la phase initiale de l'excitateur.

•	Oscillations forcées du système avec la prise en compte de l'amortissement sous l'action de la force d'attraction harmonique. Ces oscillations sont décrites par le système d'équations différentielles linéaires suivant:

ou C est la matrice carrée symétrique d'amortissement et u' est le vecteur de la vitesse des points du système. Nous supposons que le système est amorti en conformité avec la loi de Rayleigh c'est à dire qu'il est proportionnel à la distribution des raideurs et des masses du système et est définie par l'équation

où a est un rapport d'aspect de masses et b est un rapport d'aspect de rigidité (les deux ratios sont des scalaires).

•

Les oscillations forcées du système des deux types ci-dessus, nés du déplacement de supports prévus par la loi harmonique, c'est à dire apporter un système en plus de soutien pour le déplacement oscillatoire. Les équations différentielles décrivant ce type d'oscillations sont analogues à celles prévues ci-dessus mais diffèrent par la force d'attraction harmonique qui est calculé par la formule:

Plusieurs forces irrésistibles et / ou des déplacements de supports peuvent être appliquées au système, mais leurs fréquences doivent être égales.

La rotation d'un axe ou de la broche dans l'état de déséquilibre sur des supports élastiques peut servir, par exemple, de la force d'attraction harmonique. L'excitation cinématique est appliqué lorsque les valeurs des forces irrésistibles ne sont pas connus contrairement aux amplitudes des oscillations de certains éléments de structure qui sont connus.

Lors de l'analyse d'oscillations forcées, il est important de prendre en compte l'impact des forces d'amortissement. Le processus de dissipation de l'énergie des oscillations mécaniques, conduisant à l'atténuation progressive des oscillations forfaitaires produites par le système, est appelé «amortissement». Les forces d'amortissement peuvent avoir des origines différentes, à savoir:friction entre les surfaces lisses, le frottement entre les surfaces lubrifiées, la friction interne, l'air ou la résistance liquide, etc.

Il est généralement supposé que la force d'amortissement est proportionnelle à la vitesse (amortissement visqueux). Les forces de la Résistance changeante sous la loi volontaire sont remplacés par les forces d'amortissement équivalentes, en partant de la condition que en un cycle, ils dissipent la même quantité d'énergie que les forces réelles. L'équation pour les oscillations forcées avec le compte de l'amortissement pour i-ème masse, qui est la solution des équations différentielles ci-dessus, est donnée ci-dessous:

ou ω0 est la fréquence angulaire d'amortissement, ω est la fréquence angulaire de la force irrésistible.
2n=c/m ,
ou ci est facteur d'amortissement pour i-ième mode et mi est la masse.Il se compose de deux termes: l'expression entre parenthèses décrit atténuant les oscillations libres à une fréquence d'amortissement qui est peu différente de la fréquence des oscillations libres, le reste correspondant à des oscillations forcées à la fréquence d'action forcée ω.

Afin de clarifier l'impact de l'amortissement, considérons la figure qui représente le graphe de dépendance du facteur de gain des amplitudes

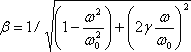
sur le rapport des fréquences d'oscillations forcées et libres ω/ω0 à des valeurs différentes du facteur d'amortissement γ=n/ω=c/ccritical , ou ccritical est le facteur critique d'amortissement visqueux, dans lequel des oscillations ne se produisent pas pendant le déplacement du système décroît de manière monotone.

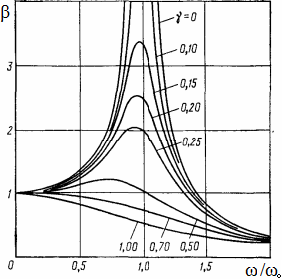
La figure montre que, lorsque la fréquence des oscillations forcées est faible en comparaison avec la même fréquence d'oscillations libre, le déplacement des points du système est approximativement égale au déplacement à la charge statique, entraînée par la force irrésistible.

Lorsque la force harmonique a une haute fréquence, indépendamment du facteur d'amortissement, il ne doit pas provoquer d'oscillations forcées du système qui a une faible fréquence propre. Dans les deux cas, ω<<ω0 et ω>>ω0, l'amortissement n'a pratiquement pas d'effet sur les oscillations forcées, mais lorsque le rapport des fréquences supérieures est d'environ 1, l'amortissement représente un impact significatif sur le facteur de gain. Avec un petit facteur d'amortissement, le plus grand impact de l'amortissement est observé près des fréquences de résonance, ce qui est crucial à considérer lors de l'analyse des structures. Aux fins de l'analyse des oscillations forcées d'une structure proche des fréquences propres, l'importation des valeurs des fréquences propres à partir des résultats de calcul de l'analyse de fréquence est fourni (voir ci-dessous).

Facteur d'amortissement γj oui j-ieme mode est liée aux rapports d'aspect a, b par l'équation
.

La valeur du facteur d'amortissement g prend des valeurs de 0,01 pour les systèmes faiblement amortis (pièces tout en métal); 0,02-0,04 (structures métalliques avec des assemblages permanents, qui sont déformés au-dessous de la limite d'élasticité), 0,03-0,07 (structures métalliques avec des connexions en coupe); 0,05 pour le caoutchouc, et jusqu'à 0,15 pour les objets fortement amorties.

Si les facteurs d'amortissement sont connus pour i- ème et j-ème modes, alors les ratios d'aspects seront calculés sous ces formules:

,
.

Si le coefficient a est égal à zéro, ces amortissement seront appelés relative et le facteur d'amortissement pour j-ème mode est proportionnelle à la fréquence angulaire de ce mode sans amortissement. Par conséquent, les oscillations correspondant à des modes plus élevés s'atténuent plus rapidement. Si le coefficient b est égal à zéro, ces amortissement seront appelés absolue, et le facteur d'amortissement pour j-ème mode est inversement proportionnelle à la fréquence angulaire de ce mode sans amortissement. Par conséquent, les oscillations correspondant à des modes inférieurs s'atténueront plus lentement.

Les principaux résultats de calcul dans le module d'oscillations forcées sont les valeurs suivantes:

•	amplitudes de déplacement aux nœuds du maillage éléments finis Um;

•	accélérations de vibration au niveau des nœuds du maillage d'éléments finis exprimé par l'amplitude Um en tant que U''m=Umω2 ;

•	surcharges de vibration, défini comme le rapport de l'accélération de vibration à l'accélération en chute libre U''m/g.

Les étapes de l'analyse des oscillations forcées

Création de "l'étude". Lors de la création d'une étude, vous devez indiquer son type, "Oscillations forcées" dans la fenêtre de propriétés. Il est possible de créer une copie de type «analyse de fréquence" de l'étude et de modifier le type, dans ce cas, les conditions de maille et de la frontière seraient transférés.

2.	Définition des matériaux. Pour définir les matériaux, il est nécessaire de cliquer sur le bouton droit de la souris sur un corps du dossier "Corps" (ou sur le dossier en soi afin de définir le même matériel pour tous les corps) et sélectionner l'option «Matériel...».

Imposer des conditions limites. Dans l'analyse des oscillations forcées, comme dans l'analyse statique, les fixations et les charges jouent le rôle de conditions limites. Dans ce type d'analyse, tous les types de fixations et les charges de force peuvent être utilisés. Imposer les fixations et les charges de la force est la condition imperative du calcul. Les limitations imposées sur le déplacement du corps doivent satisfaire la condition suivante.
Pour l'analyse statique, le modèle doit avoir une fixation pour éviter son déplacement libre dans l'espace. Le défaut de remplir cette condition aboutirait à des résultats incorrects de modélisation d'éléments finis ou l'échec du processus de calcul. Par ailleurs, la charge cinématique "oscillateur" peut remplacer les fixations partielles ou complètes.

4.	Réglage des fréquences et de l'amortissement. Effectuer des calculs. Avant le calcul, l'utilisateur doit indiquer dans les propriétés de l'étude les valeurs des fréquences de charge dont l'analyse des oscillations forcées devra être réalisée, ainsi que la valeur de l'amortissement.

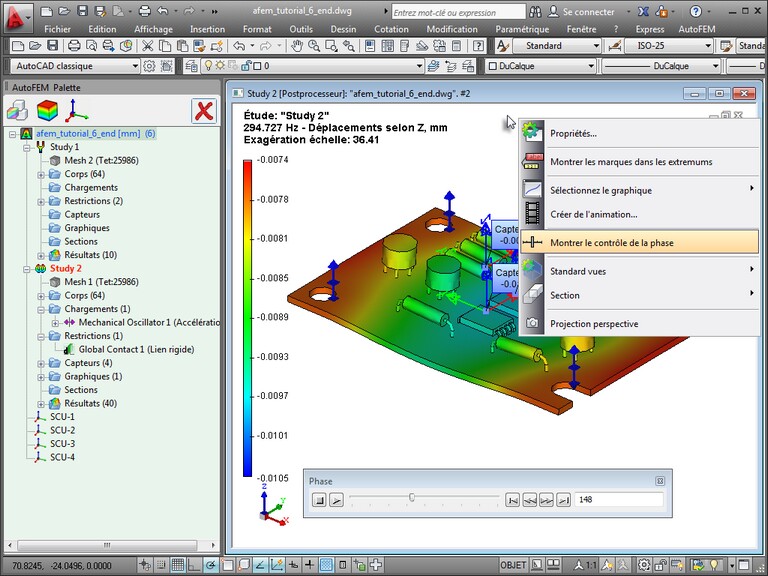
L'obtention et l'analyse des résultats. Pour affiner les résultats affichés, vous devez faire un clic droit de la souris sur le dossier de «Résultats» dans l'arbre de l'étude et sélectionner "Résultats". Les résultats de l'analyse des oscillations forcées: les amplitudes des déplacements, accélérations des vibrations ou des surcharges de vibration, et les phases d'oscillations. Pour chaque type de la "Résultat" la possibilité de voir l'état déformé d'une structure en différentes phases est prévue.

Les paramètres spécifiques à l'installation du préprocesseur dans l'analyse des oscillations forcées

1.	Réglage des limitations. Le modèle peut être limitée à la fois par des limitations complètes et partielles. Lorsque des limitations partielles sont définies, le réglage des déplacements autres que zéro est interdite.

2.	Réglage des forces. Réglage pour configurer l'amplitude des charges de force, les types de charges suivantes peuvent être appliquées à faces, des arêtes ou des vertices d'un modèle (l'accélération peut être appliqué à des corps):

•

force;

•

pression;

•	accélération;

•	charge cylindrique

•

couple.

Un certain nombre de charges influencer le système des corps simultanément, mais chacun d'entre eux aura la même fréquence. Pour chacune des charges permises, sa phase propre initiale d'oscillations peut être réglée.

Réglage de la charge cinématique (oscillateur). Pour régler l'amplitude d'oscillation du support, il faut appliquer la charge de l'oscillateur à des éléments du modèle qui peut être utilisé à la place de la fixation totale ou partielle. La charge est appliquée à faces, des arêtes ou des vertices des corps, ainsi que à des corps individuels de l'assemblage. Afin de préciser le sens des oscillations LCS est sélectionné dans la commande et la direction elle-même est indiqué par une coche, correspondant à l'axe LCS pertinente. Le type de charge cinématique est sélectionné dans la liste déroulante et pourrait être le suivant:

•	amplitude des points de déplacements;

•

vitesse;

•	accélération;

•	surcharge.

Dans le champ "Déphasage", nous pouvons régler le décalage de phase, mesurée en degrés ou en radians.

Lors de la combinaison de la charge de l'oscillateur et des fixations partielles, les directions des oscillations et des limitations doivent être différentes pour chaque élément du modèle.

Paramètres du processeur de l'analyse des oscillations forcées

Sous [Général], il est possible de déterminer ou modifier les propriétés descriptives de l'étude, c'est à dire: nom, type d'étude, et commentaires.

Dans l'onglet [Paramètres], il est possible de déterminer ou de modifier les fréquences de l'action extérieure et les paramètres d'amortissement de Rayleigh.

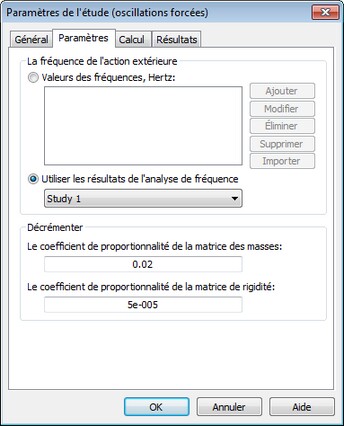
Dans le groupe de paramètres "Fréquences de l'action extérieure", les valeurs de fréquences relatives aux actions de charges externes sont établies. Il y a plusieurs façons d'ajouter de nouvelles valeurs:

1.	Le bouton [Ajouter] permet l'ajout d'une valeur unique de la fréquence ou d'une gamme de fréquences pour lequel la valeur initiale, la valeur finale et le gain sont spécifiés.

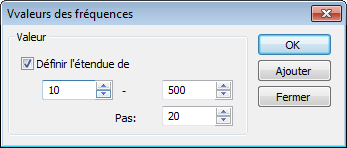
2.	Le bouton [Importer] ouvre la fenêtre de dialogue dans laquelle les valeurs de fréquences de résonance peuvent être importés sur les résultats de l'analyse de fréquence effectué plus tôt.

Quand il est nécessaire de calculer les oscillations forcées seulement à toutes les fréquences de résonance, déterminées par des analyses de fréquence précédentes, vous devez activer les éléments de contrôle "Utiliser les résultats d'analyse de fréquence". Ici, le lien associatif avec les résultats de l'analyse de fréquence sélectionnée est maintenu, c'est à dire à la variation des résultats d'analyse de fréquence, les valeurs propres de ces valeurs mises à jour seront utilisés automatiquement pour l'analyse d'oscillations forcées.

Dans la liste existante des valeurs de fréquence, les opérations d'édition suivantes sont disponibles:

•	Le bouton [Modifier] permet de ré-écrire la valeur de valeur unique spécifique;

•	Le bouton [Supprimer] supprime la valeur de fréquence sélectionnée dans la liste;

•	Le bouton [Éliminer] efface toute la liste des valeurs de fréquence.

Dans le groupe "amortissement Rayleigh", les valeurs des coefficients d'amortissement de la structure a et b sont définis.

[Calcul] permet de choisir les propriétés du processeur pour la solution d'un système d'équations. Les paramètres définissant les options du processeur sont similaires à ceux de l'analyse statique.

[Résultats] permet de déterminer les types de résultats affichés dans l'arbre d'études après le calcul.

Paramètres du post-processeur et l'analyse des résultats pour l'analyse d'oscillations forcées

Sous [Résultats], on peut voir les types de résultats répartis en huit groupes suivants:

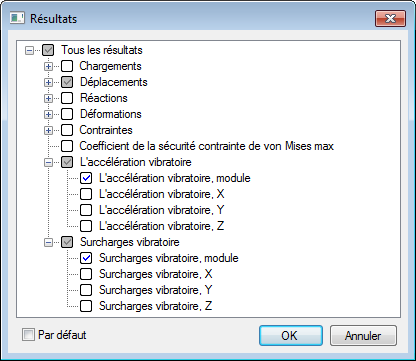
Le groupe "chargements" comprend les résultats suivants: composants utilisés pour la modélisation des éléments finis et le module de charges réduites aux nœuds. Ce type de résultats est pour la référence.Le groupe "Déplacements" comprend:

•	Les déplacements des points du modèle d'éléments finis avec prise en compte du décalage de phase par rapport à la phase d'excitation dans la direction des axes de système de coordonnées global (SC): , , , ainsi que le module de déplacement .

•	Déplacements réels dans la direction des axes du système de coordonnées (SC) global : Re(UX), Re(UY), Re(UZ), que le module des déplacements réels .

•	Une partie virtuelle de déplacement dans la direction des axes du SC global : Im(UX), Im(UY), Im(UZ), ainsi que le module de déplacements virtuels .

•	L'amplitude des déplacements des points du modèle d'élément fini (sans prise en compte du décalage de phases par rapport à la phase d'excitation) dans la direction des axes du SC global: UXm, UYm, UZm, ainsi que le module d'amplitudes .

•	Les angles de phase pour les composantes de déplacement des points du modèle d'éléments finis dans la direction des axes du SC global par rapport à la phase d'excitation

•	, , , ainsi que le module de l'angle de phase .

Dans le cas si le déphasage est réglé, nous pouvons obtenir des valeurs distinctes pour les composantes réelles et virtuelles de déplacement, ainsi que la valeur absolue de la phase dans les points du modèle d'éléments finis.

Dans le groupe "accélération de vibration", on peut noter la dérivation des valeurs des amplitudes des accélérations de vibration relatives à des points du modèle d'éléments finis U''m=Umω2 .La phase de l'accélération de vibration varie de 180 (π rad) de la phase de déplacement.

Dans le groupe "surcharges de vibrations", nous pouvons noter la dérivation de valeurs de surcharges de vibrations U''m/g, mesuré à l'égard de l'accélération en chute libre.

Aussi le graphique du résultat peut être affiché.

Retour au sommaire

autofem.com