 |
AutoFEM Analysis Theory Background | ||||||
The module “Forced oscillations” of the finite element modelling system, AutoFEM Analysis, can be used for analysing the established forced oscillations of the following types:
•Forced oscillations of the system with no account of damping under the action of harmonic compelling force. In the system with numerous degrees of freedom, these oscillations are described by the following system of linear differential equations:
![]() ,
,
where M is a symmetric square matrix of mass;
K is a symmetric square stiffness matrix of the system;
F0 is a vector of amplitudes of compelling action;
ω is frequency of compelling action;
u, u'' are vectors of coordinates of the system’s points, which change their position in time t, and their accelerations;
φ is the initial phase of the exciter.
•Forced oscillations of the system with the account of damping under action of harmonic compelling force. These oscillations are described by the following system of linear differential equations:
![]() ,
,
where C is symmetric square matrix of damping and u' is vector of velocity of the system’s points. We assume that the system is damped in accordance with Rayleigh law, i.e. it is proportional to distribution of stiffnesses and masses of the system and is defined with the equation
![]()
where a is an aspect ratio of masses and b is an aspect ratio of stiffness (both ratios are scalars).
•Forced oscillations of the system of both above types, arising from the displacement of supports under the harmonic law, i.e. bringing one ore more system supports to oscillatory displacement. Differential equations describing this type of oscillations are analogous to those set above but differ in the harmonic compelling force which is calculated via formula:![]() .
.
Several compelling forces and/or displacements of supports may be applied to the system, but their frequencies must be equal.
The rotation of a shaft or spindle in the unbalanced state on elastic supports may serve an example of harmonic compelling force. Kinematic excitation is applied when values of compelling forces are not known, in contrast to amplitudes of oscillations of some structure elements which are known.
When considering forced oscillations, it is important to take into account the impact of damping forces. The process of energy dissipation of mechanic oscillations, leading to step-by-step attenuation of lump-sum produced oscillations of the system, is termed “damping”. Damping forces may have different origin, namely: friction between dry sliding surfaces, friction between lubricated surfaces, internal friction, air or liquid resistance, etc. It is usually presumed that the damping force is proportional to velocity (viscous damping). Resistance forces changing under the voluntary law are replaced for equivalent damping forces, proceeding from the condition that in one cycle, they dissipate the same amount of energy as real forces. The equation for forced oscillations with the account of damping for i th mass, which is the solution of the above differential equations, is given below:
![]() ,
,
where ω0 is angular frequency of damping, ω is angular frequency of the compelling force.
2n=c/m ,
where ci is damping factor for i th mode; and mi is mass. It consists of two terms: expression in parentheses describes attenuating free oscillations at damping frequency which differs little from the frequency of free oscillations; the remainder corresponds to forced oscillations with the frequency of forced action ω.
In order to clarify the impact of damping, let us consider the figure which presents the graph of dependence of the gain factor of amplitudes
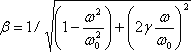
on the ratio of frequencies of forced and free oscillations ω/ω0 at differing values of the damping factor γ=n/ω=c/ccritical , where ccritical is critical factor of viscous damping, at which oscillations do not occur while the displacement of the system monotonously decays.
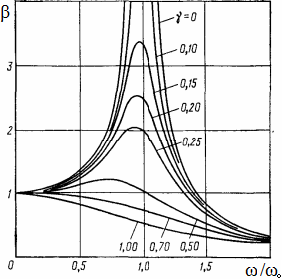
The figure shows that, when frequency of forced oscillations is low compared with the own frequency of free oscillations, the displacement of points of the system is approximately equal to the displacement at static load, driven by the compelling force. When the driving harmonic force has high frequency, than regardless of the damping factor, it does not cause forced oscillations of the system, which has low own frequency. In both cases ω<<ω0 and ω>>ω0, damping does not virtually impact the forced oscillations, albeit when the ratio of the above frequencies is about 1, than damping poses a significant impact on the gain factor. At small damping factor, the greatest impact of damping is observed near resonance frequencies, which is crucial to consider when analysing the structures. For purposes of analysing forced oscillations of a structure near own frequencies, import of values of own frequencies from the results of computation of the frequency analysis is provided (see below).
Damping factor γj for j th mode is tied to aspect ratios a, b by the equation
![]() .
.
The value of the damping factor γ takes values from 0.01 for weakly damped systems (all-metal parts); 0.02-0.04 (metal structures with permanent joints, which are deformed below the yield strength); 0.03-0.07 (metal structures with in-cut connections); 0.05 for rubber; and up to 0.15 for strongly damped systems.
If damping factors are known for i th and j th modes, than aspect ratios will be calculated under formulas:
![]() ,
,
![]() .
.
If the coefficient a is equal to zero, such damping will be called relative, and the damping factor for j th mode will be proportional to angular frequency of that mode without damping. Therefore, oscillations corresponding to higher modes will attenuate faster. If the coefficient b is equal to zero, such damping will be termed absolute, and the damping factor for j th mode will be inversely proportional to angular frequency of this mode without damping. Therefore, oscillations corresponding to lower modes will attenuate slower.
The main results of calculation in the module of forced oscillations are the following values:
•amplitudes of displacement at finite element mesh nodes Um;
•vibration accelerations at finite element mesh nodes expressed via amplitudes Um as U''m=Umω2 ;
•vibration overloads, defined as the ratio of vibration acceleration to free fall acceleration U''m/g.
See also: Forced Oscillation Analysis, Specific Pre-Processor Settings, Steps of Oscillation Analysis, Settings of Oscillation Solver, Analysing Results