 |
 |
 |
 |
 |
 |
AutoFEM Analysis Axiale und transversale Schwingungsfrequenz eines Strahls mit einem Gewicht |  |
|
|
|
|
|
|
AutoFEM Analysis Axiale und transversale Schwingungsfrequenz eines Strahls mit einem Gewicht | |
Axiale und transversale Schwingungsfrequenz eines Strahls mit einem Gewicht
Betrachten wir den Auslegerbalken, der rechte Ende sich unter dem Gewicht ist.
|
Die Länge des Balken ist L. Der Querschnitt des Balkens ist ein Rechteck mit einer Breite b und Höhe h. Die Masse des Gewichtes ist M. Die spezifische Masse des Balkens ist m.
m = ρ F,
wo F = b h, ρ ist die Dichte des Materials des Trägers.
|
Die Finite-Elemente-Modell mit Lasten und Beschränkungen |
Angenommen L = 0.5 m, b = 0.05 m, h = 0.02 m.
Die wesentlichen Eigenschaften sind: der Young-Modul E = 2.1E+011 Pа, Poissonzahl ν=0.28, die Dichte ρ = 7800 kg / m3.
Die Masse des Gewichts M gleich 2.m.L kg (i.e. 7.8 kg).
Analytische lösung dieses Problems ist durch die folgenden Formeln gegeben:
a) die axiale Schwingungsfrequenz
b) die transversale Schwingungsfrequenz
,
.
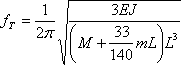Somit, fA = 1078.962 Hz , fT = 22.092 Hz.
Nach Durchführung Berechnung mit Hilfe der AutoFEM, werden die folgenden Ergebnisse erzielt:
Tabelle 1. Parameter der Finite-Elemente-Netz
Art der Finite-Elemente |
Anzahl der Knoten |
Anzahl der finiten Elementen |
quadratische Tetraeder |
2173 |
8719 |
Tabelle 2. Ergebnis "Frequenz"*
Numerische Lösung |
Analytische Lösung |
Fehler δ = 100%*| fi* - fi| / | fi | |
22.235 |
22.092 |
0.65 |
1080.013 |
1078.962 |
0.002 |
|
|
*Die Ergebnisse der numerischen Untersuchungen hängen von der Finite-Elemente-Netz und können geringfügig von den in der Tabelle angegeben.
Lesen Sie mehr über AutoFEM Frequency Analysis
