Erzwungenen Schwingung eines Feder-Masse-System

Betrachten wir ein Feder-Masse-System (siehe Abbildung). Dieses mechanische System ist ein klassisches Beispiel für eine Schwingung mit einem Freiheitsgrad. Das Verhalten des Systems ist gut untersucht und kann durch trigonometrische Funktionen, die in klassischen physikalischen und mechanischen Lehrbüchern betrachtet werden beschrieben.

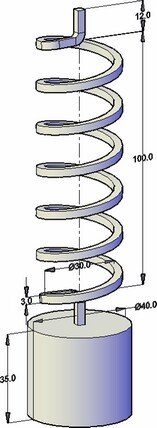
Lassen Sie die vertikale harmonische Kraft auf die Masse und der Bewegung der Masse wird nur entlang der Z-Achse (vertikal) erlaubt wird. Die Kraft mit der Zeit variiert durch harmonische Gesetz:

F(t)=F0sin(ωft),

wo  F0 ist gleich 10 N.

ωf= 2π ff ,

wo die Frequenz ff reicht von 5Hz bis 30Hz.

Unser Ziel ist es Schwingungsamplituden der Masse unter Verwendung der angegebenen Frequenzen zu finden.

Lassen Sie uns die folgenden ersten Daten: der mittlere Durchmesser der Feder D beträgt 30 mm, die Länge der Feder H beträgt 100 mm, der Querschnitt des Drahtes ist ein Quadrat mit einer Seitenlänge d = 3 mm, die Anzahl der Federwindungen n ist. Parameter mit einem Gewicht sind folgende: der Durchmesser DW= 40 mm, H = 35 mm, Masse mW= 0.34306 kg.

Parameter der Feder/Gewicht Material: Elastizitätsmodul E=2.1E+011Pa, Poissonzahl ν=0.28, Dichte ρ=7800kg/m3, Schubmodul G=8.203E+010Pa, Dämpfungskoeffizient 2 % relativ die kritischen Dämpfung.

Klassische analytische Lösung

Amplitude gezwungen Oberschwingungen für das System mit einem Freiheitsgrad wird gemäß nächsten Ausdruck beschrieben

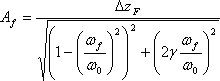                       (1)

wo ΔzF ist eine Verschiebung unter statischen Kraftwirkung, die gleich Amplitude der harmonischen Antriebskraft, ωf = 2*π*ff ist zyklisch Frequenz treibende Kraft, ω0 = 2*π*f0 ist eine eigene Frequenz; γ=c/ccr=0.02 ist die relative Dämpfungskoeffizient. Freie Oszillationsfrequenz des Gewichts mit der Feder, die als ein System mit einem Freiheitsgrad betrachtet werden, wird als nächstes bekannten Formel ermittelt:

                                       (2)

wo g ist frei Fallbeschleunigung, m/s2; Δz ist die statische Verschiebung der Masse aufgrund der Schwerkraft Aktion.

Statische Verschiebung ist definiert als [2]:

                               (3)

wo m ist die Masse des Gewichts, kg.

Das Ergebnis der Lösung der Gleichung (3) ergibt statischer Verlagerung des Gewichts aufgrund Schwerkraftwirkung

Δzg=0.451 mm.

Somit, die analytische Lösen von Gleichung (2) ergibt nächsten Wert der Frequenz für betrachteten Systems mit einem Freiheitsgrad: f0 = 23.457 Hz.

Die Verschiebung des freien Endes der Feder unter statischer Last kann durch die folgende Formel berechnet werden:

Somit, statische Deformation unter der statischen Belastung ΔzF = 1.342 mm . Wenn die Resonanz auftritt (ff = f0), die Schwingungsamplitude gleich Af=ΔzF/2γ = 33.55 mm.

Numerische Lösung

Lassen Sie uns lösen dieses Studie AutoFEM Analysis Paket. Das obere Ende der Feder befestigt ist vollständig. Verschiebung des Gewichts längs der X-Achse und Y-Achse sind verboten.

Die statische Verschiebung des Systems unter dem Gewicht ist Δz*g = 0.428 mm (das Ergebnis "Verschiebung OZ" der Studie "Static Analysis (gravity)").

Erste Eigenfrequenz gleich f(1)c =23.594 Hz (das Ergebnis "Mode 01 (23.594 Hz)" der Studie "Frequency Analysis").

Die Verschiebung des freien Endes der Feder unter statischer Last ist gleich Δz*F = 1.288 mm (das Ergebnis "Verschiebung OZ" der Studie "Static Analysis (force)").

Lassen Sie die Verhältnisse der Rayleigh Dämpfung haben folgende Werte: α= 0.02, β= 2.6891E-004. Diese Werte bis 2% des kritischen Widerstands entsprechen.

Der Dämpfungskoeffizient γ kann durch folgende Formel definiert werden:

Die Schwingungs-Resonanz-Amplitude hat den folgenden Wert: A*f=32.19 mm .

Vergleichen wir die Ergebnisse der Berechnung:

Tabelle 1. Parameter der Finite-Elemente-Netz

Tabelle 2. Die Ergebnisse

 

 

*Die Ergebnisse der numerischen Untersuchungen hängen von der Finite-Elemente-Netz und können geringfügig von den in der Tabelle angegeben.

 

Lesen Sie mehr über  AutoFEM Oscillations Analysis

Zurück zum Inhaltsverzeichnis