Schwingungen eines Feder-Masse-System, weil der schwingenden Fundament

Betrachten wir die Masse-Feder-System. Die Feder vibrierendem Untergrund befestigt ist, sind Schwingungen von denen harmonisch. Die Amplitude der Schwingung ist gleich 1.34192762 mm.

Lassen Sie uns die folgenden ersten Daten: der mittlere Durchmesser der Feder D beträgt 30 mm, die Länge der Feder H beträgt 100 mm, der Querschnitt des Drahtes ist ein Quadrat mit einer Seitenlänge d = 3 mm, die Anzahl der Federwindungen n ist. Parameter mit einem Gewicht sind folgende: der Durchmesser DW= 40 mm, H = 35 mm, Masse mW= 0.34306 kg.

Parameter der Feder/Gewicht Material: Elastizitätsmodul E=2.1E+011Pa, Poissonzahl ν=0.28, Dichte ρ=7800kg/m3, Schubmodul G=8.203E+010Pa, Dämpfungskoeffizient 2 % relativ die kritischen Dämpfung.

Unser Ziel ist es Schwingungsamplituden der Masse zu finden, mit den Frequenzen, die von 5Hz bis 30Hz reicht. Lassen Sie die Verhältnisse der Rayleigh Dämpfung haben folgende Werte: α= 0.02, β= 2.6891E-004. Diese Werte bis 2% des kritischen Widerstands entsprechen.

Amplitude gezwungen Oberschwingungen für das System mit einem Freiheitsgrad wird gemäß der folgenden Formel beschrieben:

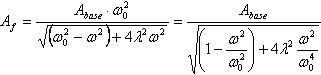,                (1)
wo Abase -eine Amplitude der Schwingung der Basis, ω ist die Frequenz der Schwingungen der Basis, ω0 ist die natürliche Kreisfrequenz der Schwingungen des Systems, λ ist der Dämpfungskoeffizient.

Bezeichnen wir den Ausdruck λ/ω0= γ, dann wird die Formel (1) übergeht:

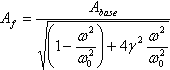,                                        (2)
wo der Koeffizient γ wird durch die folgende Formel berechnet werden:

.                                                (3)

Die Koeffizienten α, β  ​​sind die Masse Dämpfungskoeffizient und die Steifigkeit Dämpfungskoeffizienten.

Die Federsteifigkeit wird durch die Formel berechnet wird:
.                                                        (4)

Somit, die Feder hat Steifigkeit:
.

Dann wird der natürliche Kreisfrequenz
,
und die natürliche Frequenz ist
.

Wir berechnen die Amplituden A f durch die Formel (2) für die Frequenzen f1=5Hz, f2=10Hz, f3=15Hz, f4=20Hz, f5=f0, f6=25Hz, f7=30Hz and γ=0.02.

Somit, A1f= 1.4057 mm, A2f= 1.6396 mm, A3f= 2.2682 mm, A4f=4.8773 mm, A5f= 33.8482 mm, A6f= 9.4208 mm, A7f= 2.1041 mm.

Lassen Sie uns zu lösen diese Studie mit AutoFEM Analysis.

Das obere Ende der Feder ist mit der Amplitude gleich oszillierenden 1.34192762 mm. Verschiebung des Gewichts längs der X-Achse und Y-Achse sind verboten.

Nach Durchführung Berechnungen des AutoFEM Analyse folgende Ergebnisse erhalten:

Tabelle 1. Parameter der Finite-Elemente-Netz

Tabelle 2.Ergebnis “Amplitude”

 

 

*Die Ergebnisse der numerischen Untersuchungen hängen von der Finite-Elemente-Netz und können geringfügig von den in der Tabelle angegeben.

 

Lesen Sie mehr über  AutoFEM Oscillations Analysis

Zurück zum Inhaltsverzeichnis