Thermischen Kontakt zwischen einfachen Platten

 

Wir betrachten die Aufgabe des stationären Wärmestroms in dem Komplex Platte mit  Breite ∑hi und Wärmeleitfähigkeit Koeffizienten ki, dessen erster und letzter Oberfläche aufrechtzuerhalten Temperaturen t1 und tn+1 und zwischen den Platten mit den Zahlen m-1 und m+1, besteht ein thermischer Kontakt mit einem spezifischen Widerstand Rm (siehe Abbildung).

The temperature change and heat flux along the width of the complex plate, consisting of n sheets with widths h1, h2,... hn and thermal conductivity coefficients k1, k2,... kn , respectively, for each sheet, fi, i=1,2,..., n are defined using the formula:

Die Temperaturänderung und Wärmefluss entlang der Breite des Komplexes Platte, bestehend aus n Bögen mit Breiten h1, h2,... hn und Wärmeleitfähigkeit Koeffizienten k1, k2,... kn jeweils für jedes Blatt, fi, i=1,2,..., n werden mit Hilfe der Formel:

Lassen Sie alle Blätter, speichern zwei Einsen, sind in der idealen thermischen Kontakt entlang Grenzflächen. Angenommen thermischen Widerstand Rm zwischen Lagen nummerierten m-1 und m+1, dann wird der Wärmestrom wird am Übergang von einem Bereich in den anderen ununterbrochenen, und in diesem Fall, wird die gleiche sein, in jedem Punkt (f1=f2=...=fn=f). Die Veränderung der Temperatur zwischen den gegenüberliegenden Oberflächen des gesamten Komplexes Platte wird gleich der Summe der Temperaturänderungen in getrennten Blättern:

Dann:

,

 

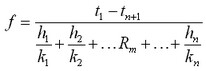
Lassen Sie akzeptieren die folgenden anfänglichen Daten: Anzahl der Blätter ist n=2,Länge und Breite jedes Blattes sind 100 mmund 50 mm, und Breiten der Blätter h1, h2, sind 8 mm, 10 mm. Die angewandten Temperaturen t1und t2 gleich 373K und 273K.

Wärmeleitfähigkeit Koeffizienten sind:

,

Wärmedurchlasswiderstand des Kontakts

(es ist ungefähr gleich dem thermischen Widerstand des unformatierten Luftschicht mit der Breite 0.05 mm mit

)

Somit,
.

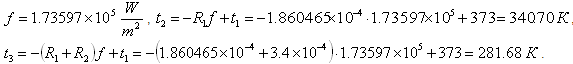
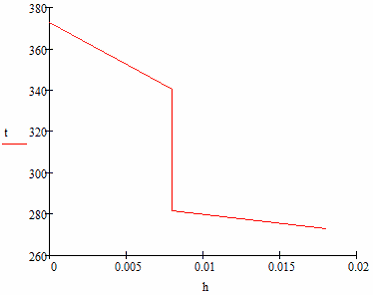
Durch Berechnung mit Hilfe der AutoFEM Analyse haben wir die folgenden Ergebnisse (für den unteren und oberen Seiten der Kontaktbrücke jeweils) erhalten:

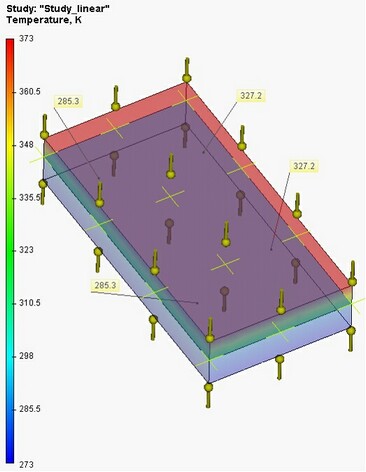
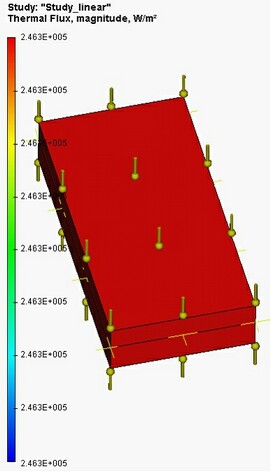
Tabelle 1.*

Tabelle 2.*

 

 

*Die Ergebnisse der numerischen Untersuchungen hängen von der Finite-Elemente-Netz und können geringfügig von den in der Tabelle angegeben.

 

Lesen Sie mehr über  AutoFEM Thermal Analysis

Zurück zum Inhaltsverzeichnis