 |
AutoFEM Analysis Axial Vibration Frequency and Transverse Vibration Frequency of the Beam with a Weight | ||||||
 |
AutoFEM Analysis Axial Vibration Frequency and Transverse Vibration Frequency of the Beam with a Weight | ||||||
Vibración axial y transversal en la Frecuencia de una viga con un peso
Consideremos la viga en voladizo, el extremo derecho de los cuales es bajo el peso.
|
La longitud de la viga es L. La sección transversal del haz es un rectángulo de anchura b y la altura h. La masa del peso es M. La masa específica de la viga es m.
m = ρ F,
Donde F = b h, ρ es la densidad del material de la viga.
|
El modelo de elementos finitos con cargas y restricciones |
Tenemos que L es igual to 0.5 m, b es igual to 0.02 m, h es igual to 0.05 m.
Las propiedades del material son: el módulo de Elasticidad E = 2.1E+011 Pа, El coeficiente de Poisson ν=0.28,
la densidad ρ = 7800 kg / m3.
La masa del peso es Igual a M 2.m.L kg (i.e. 7.8 kg).
Solución analítica de este problema viene dada por las siguientes fórmulas:
a) La Frecuencia de vibración axial
![]()
b) La frecuencia de vibración transversal
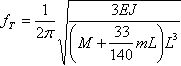 ,
,
![]() .
.
Así, fA = 1078.962 Hz , fT = 22.092 Hz.
Después de llevar a cabo el cálculo con la ayuda de AutoFEM, se obtienen los siguientes resultados:
Tabla 1. Parámetros de malla de elementos finitos
Tipo de elementos finitos. |
Número de Nodos |
Número de elementos finitos. |
tetraedro cuadrática |
4086 |
2168 |
Tabla 2. Resultado "Frecuencia"
Solución numérica. |
Solución analítica |
Error δ = 100%*| fi* - fi| / | fi | |
22.235 |
22.092 |
0.65 |
1080.407 |
1078.962 |
0.13 |
|
|
Conclusiones:
El error relativo de la solución numérica. en comparación con la solución analítica no exceda 0.7%.
Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.
Lea más acerca de AutoFEM Frecuencia Analysis