Oscilación forzada de un sistema resorte-masa

Consideremos un sistema de resorte-masa (véase la figura). Este sistema mecánico es un ejemplo clásico de un sistema de oscilación con un grado de libertad. El comportamiento de este sistema está bien estudiado y puede ser descrito por las funciones trigonométricas elementales que se consideran en los libros de texto físicos y mecánicos clásicos.

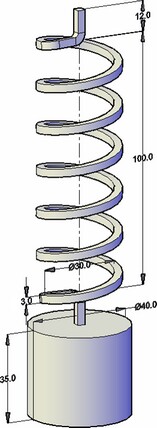
Deja que la fuerza armónica vertical se aplica a la masa y el movimiento de la masa se ​​deja de ser sólo en el eje Z (vertical). La fuerza varía con el tiempo por la ley armónica:

F(t)=F0sin(ωft),

Donde  F0 es igual to 10 N.

ωf= 2π ff ,

Donde los rangos de frecuencia son ff  5Hz to 30Hz.

Nuestro objetivo es encontrar amplitudes de oscilación de la masa utilizando las frecuencias especificadas.

Vamos a usar los siguientes datos inicial: el diámetro medio del resorte de D es 30 mm, la longitud del resorte de H es de 100 mm, la sección transversal del alambre es un cuadrado con un lado d = 3 mm, el número de primavera resulta n es 6. Parámetros de un peso son los siguientes: el diámetro DW= 40 mm, altura H=35 mm, masa mW= 0.34306 kg.

Parámetros del material de resorte / peso: módulo de elasticidad E=2.1E+011Pa, El coeficiente de Poisson ν=0.28, densidad ρ=7800kg/m3, módulo de corte G=8.203E+010Pa, coeficiente de amortiguación 2% relativamente la amortiguación Crítica.

Solución analítica clásica

Amplitud de oscilaciones armónicas forzadas para el sistema con un grado de libertad se describe según la expresión siguiente

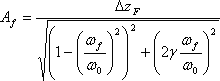                       (1)

Donde ΔzFes un desplazamiento bajo la acción de fuerzas estáticas, que de es Igual a la amplitud de la fuerza de conducción armónica, ωf = 2*π*ff , ω0 = 2*π*f0- frecuencia cíclica de fuerza motriz y propia frecuencia relativamente; γ=c/ccr=0.02 - coeficiente de amortiguación relativa. Oscilación de libre frecuencia del peso con el muelle, que se consideran como un sistema con un grado de libertad, se determina de la siguiente famosa expresión [1]:

                                       (2)

Donde g –

la aceleración de caída libre, m/s2; Δz – Desplazamiento estático de la masa debido a la acción de la gravedad.

Desplazamiento estático se define como [2]:

                               (3)

Donde m – peso de la masa, kg;  D – diámetro medio del muelle, mm;  n – el número de vueltas del resorte; d – la sección transversal del alambre, mm; G – módulo de corte, Pa.

El resultado de la ecuación, (3) da Desplazamiento estático del peso debido a la acción de la gravedad

Δzg=0.451 mm.

Así, la solución analítica de la ecuación (2) da siguiente valor de frecuencia para el sistema considerado, con un grado de libertad: f0 = 23.457 Hz.

El desplazamiento del extremo libre del muelle bajo carga estática se puede calcular por la siguiente fórmula:

Donde F es una fuerza axial, N; D es el diámetro medio del muelle, mm; n es el número de espiras del resorte, d es el tamaño del cable, mm; G es el módulo de cizallamiento, Pa.

Así, Deformación estática bajo la carga ΔzF = 1.342 mm . Si se produce la resonancia (i.e. ff = f0), La vibración de la amplitud es igual a Af=ΔzF/2γ = 33.55 mm.

Solución numérica.

Vamos a resolver este estudio por paquete AutoFEM Análisis. El extremo superior del muelle está completamente fija. Se prohiben desplazamientos del peso a lo largo del eje X y el eje Y.

El Desplazamiento estática del sistema bajo el peso adecuado es Δz*g = 0.428 mm (el resultado "Desplazamiento OZ" del estudio "Análisis estático (la gravedad)").

La primer frecuencia es igual a  f(1)c =23.594 Hz (El resultado del módulo es 01 (23.594 Hz)" del estudios de frecuencia "análisis de frecuencia").

El desplazamiento del extremo libre de la primavera bajo estática Igual es la carga de Δz*F = 1.288 mm (los resultados de "Desplazamiento OZ "del estudio" análisis estático (fuerza) ").

Deje que las proporciones de la amortiguación Rayleigh tienen los siguientes valores: α= 0.02, β= 2.6891E-004. Estos valores corresponden a 2% de la la resistencia crítica.

El coeficiente de amortiguación g puede ser definido por la fórmula siguiente:

La amplitud de resonancia vibracional tiene el siguiente valor: A*f=32.19 mm .

Vamos a comparar los resultados de cálculo:

Tabla 1. Parámetros de la la malla de elementos finitos

Tabla 2. Los resultados

 

 

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

 

Lea más acerca de AutoFEM Oscillations Analysis

autofem.com

Volver al índice