Las vibraciones de un sistema resorte-masa debido fundación oscilante

Consideremos el sistema de masa-resorte. El muelle está unido a la base de vibración, las vibraciones de los cuales son armónica. La amplitud de la oscilación es Igual a 1.34192762 mm.

Vamos a usar los siguientes datos inicial: el diámetro medio del resorte de D es 30 mm, la longitud del resorte de H es de 100 mm, la sección transversal del alambre es un cuadrado con un lado d = 3 mm, el número de primavera resulta n es 6. Parámetros de un peso son los siguientes: el diámetro DW = 40 mm, altura H = 35 mm, la masa mW = 0.34306 kg.

Parámetros del material de resorte / peso: módulo de elasticidad E=2.1E+011Pa, El coeficiente de Poisson ν=0.28, densidad ρ=7800kg/m3, módulo de corte G=8.203E+010Pa, coeficiente de amortiguamiento 2 % relativamente la amortiguación Crítica.

Nuestro objetivo es encontrar amplitudes de oscilación de la masa, utilizando las frecuencias que va desde 5Hz a 30Hz. Las proporciones de la amortiguación de Rayleigh han siguientes valores: α= 0.02, β= 2.6891E-004. Estos valores corresponden a 2% de la resistencia Crítica.

Amplitud de las oscilaciones armónicas forzada para el sistema con un grado de libertad se describe de acuerdo con la siguiente fórmula:

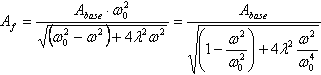,                (1)
Donde Abase es una amplitud de oscilación de la base,ω es la Frecuencia angular de las oscilaciones de la base, ω0es la Frecuencia angular natural de las oscilaciones del sistema, λes el coeficiente de amortiguación.

Denotemos la expresión λ/ω0= γ, entonces la fórmula (1) pasa por encima:

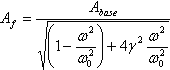,                                        (2)
Donde el coeficiente de g se calcula por la siguiente fórmula:

.                                                (3)

Los coeficientes α, β son el coeficiente de amortiguación de masas y el coeficiente de rigidez de amortiguación, respectivamente.

La rigidez del resorte se calcula por la fórmula:
.                                                        (4)

Asi, el resorte haya la rigidez siguiente:
.

A continuación, la Frecuencia angular natural es
,
y la frecuencia natural es.
.

Vamos a calcular las amplitudes A f por la fórmula (2)  para las frecuencias f1=5Hz, f2=10Hz, f3=15Hz, f4=20Hz, f5=f0, f6=25Hz, f7=30Hzyγ=0.02.

Así, A1f= 1.4057 mm, A2f= 1.6396 mm, A3f= 2.2682 mm, A4f=4.8773 mm, A5f= 33.8482 mm, A6f= 9.4208 mm, A7f= 2.1041 mm.

Vamos a resolver este estudio por Análisis AutoFEM.

El extremo superior del muelle está oscilando con una amplitud igual a 1.34192762 mm. Se prohiben desplazamientos del peso a lo largo del eje X y el eje Y.

Después de la realización de los cálculos por el Análisis AutoFEM se obtienen los siguientes resultados:

Tabla 1. Parámetros de la malla de elementos finitos

Tabla 2.El resultado de “Amplitud”

 

 

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

 

Lea más acerca de AutoFEM Oscillations Analysis

autofem.com

Volver al índice