 |
 |
 |
 |
 |
 |
AutoFEM Analysis Placa isotrópica bajo flujo de calor y convección |  |
|
|
|
|
|
|
AutoFEM Analysis Placa isotrópica bajo flujo de calor y convección | |
Placa Isotrópica bajo flujo de calor y convección
Consideremos una placa de acero bxa = 100x200 mm de espesor D = 5 mm con la conductividad térmica de K = 50 W / (m oK) [aleación de acero (SS)]. Vamos a mostrar que el problema de la transferencia de calor en estado estacionario también puede resolverse para el caso de que en el límite de la temperatura no se mantiene constante (para el modelado de la temperatura correcta debe ser conocida de antemano). Vamos a considerar dos tipos de cargas: flujo de calor (igual a cero para algunos límites) de transferencia de calor y por convección. En la superficie de la placa (de ambos lados) prescribimos el intercambio de calor con el entorno ambiental con el coeficiente de transferencia de calor C=40 W/(m2 • oK) y la temperatura del medio ambiente igual a cero. En el cuarto lado (de 100 mm de longitud) prescribimos una transferencia de calor por convección con el coeficiente H=20 W/(m2 • oK) y la temperatura del entorno ambiental es igual a u0=283.15 oK. (ver la figura).
|
Vamos a localizar el origen del sistema de coordenadas en la esquina de la placa, dejar que el eje O y se dirige a lo largo del lado más largo de la placa, y convección entonces se aplica al borde y = b. A continuación vamos a inferir que dos de cada tres bordes, en los que se prescribe un flujo de calor cero, corresponden a los valores x = 0yx = a. Esto significa que la solución que se obtiene no tiene que depender de la coordenada x. Solución tendrá la forma:
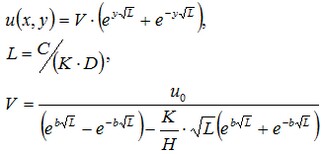
A continuación les mostramos las líneas isotérmica para la solución obtenida mediante el software de arce.
La convección es aplicado para la coordenada Y=b.
|
|
líneas isotérmicas para la solución obtenida mediante el software de arce. La convección se aplica al borde y = b. Cuando y = 0 el flujo de calor térmico es cero |
Vamos a localizar los sensores de la temperatura como se muestra en la figura y crea un complot para ellos en y = 170; 180; 190; 200 mm. En los puntos dados compararemos la Solución numérica. obtenido utilizando el Análisis AutoFEM con la solución analítica.
|
|
El modelo de elementos finitos con condiciones de frontera aplicados |
Después de llevar a cabo el cálculo se obtienen los siguientes resultados:
Tabla 1. Parámetros de malla de elementos finitos
Tipo de elementos finitos. |
Número de Nodos |
Número de elementos finitos. |
Tetraedro lineal |
462 |
1200 |
Tabla 2. Resultado " temperatura "
Coordinate y, mm |
Solución numérica. |
Solución analítica |
Error δ = 100%* |T* - T| / |T| |
170 |
273.2773 |
273.2783 |
3.55E-04 |
180 |
273.3029 |
273.3033 |
1.43E-04 |
190 |
273.3325 |
273.3332 |
2.67E-04 |
200 |
273.3669 |
273.3690 |
7.86E-04 |
|
Conclusiones:
El error relativo de la solución numérica. en comparación con la solución analítica no exceda 0,0008% para los elementos lineales.
El problema se resolvió casi exactamente con el mínimo coste computacional.
Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.
Lea más acerca de AutoFEM Térmico Analysis
