Flujo térmico  de calor en un disco Isotrópico

Consideremos ahora el problema de calentamiento de una placa circular con las fuentes de calor distribuidos sobre la superficie. Vamos a prescribir el flujo de calor desde ambos lados. Alrededor de la placa a lo largo de los bordes vamos a prescribir la constante de  temperatura .

Como ejemplo consideramos una placa delgada con la térmica conductividad K = 75 W / (m • OK) [Hierro Dúctil (SN)]. El radio de la placa es de R = 100 mm, grosor D = 5 mm. El valor de la densidad del flujo de calor es F = 60 W/m2.  temperatura  de los bordes alrededor de la placa es T = 293,15 o K. (ver la Figura).

La ecuación que hay que resolver para una superficie de un disco tiene la siguiente forma:

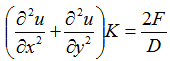
En el lado derecho de la ecuación tenemos la densidad volumétrica de la fuente de calor (equivalente a una densidad de superficie para un problema plano).

Condiciones de contorno:

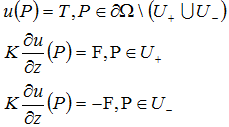
Donde U- y U+ - son lados respectivamente inferior y superior de la placa. Solución analítica se puede expresar en términos de la función de la fuente de calor G(P, P0).

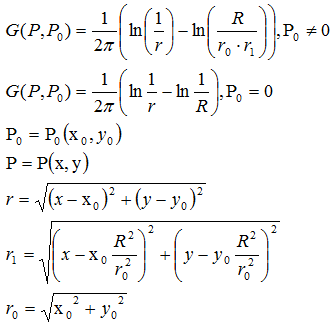
Esta función es una solución de la ecuación de Laplace con el lado derecho singular (en la parte derecha tenemos la función de Dirac) de potencia unitaria.

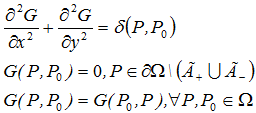
Solución de la ecuación de Poisson se puede expresar en términos de la función de fuente como:

 

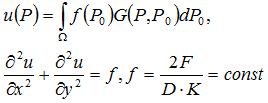
Solución analítica se calculó en el sistema de arce 9.5 por el método de integración numérica _d01ajc (integración Gauss utilizando 10 puntos y la integración Croncord utilizando 21 puntos). Utilizamos 6 dígitos significativos de precisión en la Analítica Solución para comparar la Resultados.

Vamos a localizar los sensores de la  temperatura  como se muestra en la figura y hacer un complot para ellos en r = 0; 20; 40; 60 mm. En los puntos dados compararemos la Solución numérica. obtenido utilizando el Análisis AutoFEM con la solución analítica.

Después de llevar a cabo el siguiente cálculo se obtiene los siguiente resultados:

Tabla 1. Parámetros de malla de elementos finitos

Tabla 2. Resultado " temperatura "

 

Conclusiones:

El error relativo de la solución numérica. en comparación con la solución analítica no exceda 0,0008% para los elementos lineales.

El problema se resolvió casi exactamente con el mínimo coste computacional. Es importante tener en cuenta que en un punto r = 20 mm la solución con elementos lineales resulta ser más preciso. Esto fue realmente posible debido a las propiedades de convergencia de la solución en el método de elementos finitos (convergencia en un sentido de la norma integral y menor número de puntos / argumentos juega un papel aquí). Sin embargo, en general, es imposible predecir la apariencia y la ubicación de estos puntos.

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

 

Lea más acerca de AutoFEM Térmico Analysis

autofem.com

Volver al índice