La radiación de una placa en el entorno exterior

Consideremos ahora un problema de cálculo del campo  temperatura  de estado estacionario para una placa plana infinita que irradia al entorno externo. En los bordes de la placa (a lo largo de la longitud), mantenemos la constante de  temperatura  T = 500 OK (suponemos que para este  temperatura  el efecto de la radiación de esta placa será significativo). La radiación se llevará a cabo a partir de la superficie de la placa a ambos lados de la placa para el medio ambiente externo con la igualdad de  temperatura ext = 293o. Ahora suponiendo que el estado de equilibrio, podemos determinar el campo  temperatura  en la superficie de la placa en los puntos de control que han sido designados por los sensores (ubicados a lo largo del eje OХ).

Características de la placa: espesor d = 5 mm, ancho l = 100 mm; Térmica conductividad K = 50 W / (m • O K); emisividad α = 1. Mantenemos el flujo de calor a cero a lo largo de la frontera de una anchura de la placa. (ver la Figura).

 

Consideremos la ecuación diferencial para este problema. Dado que el flujo de calor térmico en los bordes opuestos de la placa es Igual a cero, el campo  temperatura  va a cambiar sólo a lo largo de la longitud de la placa. Al seleccionar el sistema de coordenadas de tal manera que el eje OX se dirige a lo largo de la anchura de la OY-eje plateythe a lo largo de la longitud, obtendremos la solución que depende sólo de la anchura de la placa. Pondremos el origen del sistema de coordenadas О en el centro de la placa. La ecuación tomará la forma:

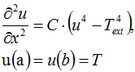
Donde la constante С se determina tomando en cuenta la anchura de la placa como:

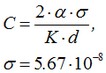
Donde σ – constante de Boltzmann.

La Analítica Solución para este problema se puede encontrar como desarrollo en serie de Taylor. También se puede conseguir numéricamente en el sistema de arce 9.5. Tendremos en cuenta el valor a lo largo de la longitud sólo hasta el punto medio, es decir, el origen seleccionado del sistema de coordenadas, ya que la solución es una función par (desde el punto de vista físico, es obvio porque tenemos igual  temperatura  largo de los bordes y el material es isótropo. En el centro tendremos el punto de mínima ya que el cuerpo pierde calor).

Vamos a representar ahora el Analítica Solución para el problema como una serie. Tomamos nota de que

ya que desde el punto de vista físico la placa no podría enfriar hasta la  temperatura  por debajo de la  temperatura  del entorno ambiental. Por lo tanto, ∂u/∂x crece de forma monótona desde -  to + y que significa que tiene un único punto de intersección con el eje OX que será el punto de mínimo de la solución. En los alrededores de este punto nos expandimos la solución de una serie:

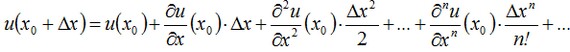
Al diferenciar la ecuación dada, obtendremos las expresiones para las derivadas de orden superior:

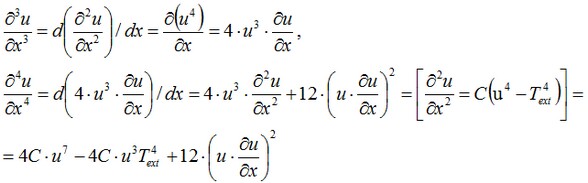
y así sucesivamente. Es obvio que todos los derivados pueden ser representados en forma de un polinomio f de valores de la función u y de su primera derivada

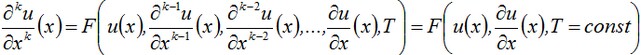
todos los derivados impares, todos los términos del polinomio f contendrán como un factor de la primera derivada y por lo tanto en el punto de extremo tenemos

De ahí que la solución tendrá la forma:

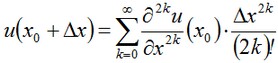
Es obvio a partir de la simetría de las condiciones de contorno que el punto x0 coincide con el O cero seleccionado del sistema de coordenadas.

No existe una sencilla analítica Solución para desde en cada paso de cálculo de la suma de la serie, que necesitamos para almacenar todos los coeficientes de polinomio f para evaluar el derivado para el siguiente paso. Que es por lo que usamos formas estándar de evaluación analítica del derivado a través del sistema de arce 9.52*.

El valor de u en un punto x0 se obtuvo de la siguiente manera: seleccionados las sumas parciales de series de Taylor en un punto x0 + l/2yequate que el valor límite de la T. La solución de estas ecuaciones  temperatura  se puede encontrar numérica y , por otra parte, sólo las raíces positivas reales eran de interés. Como resultado se obtuvo u (0) = 467.4671303.

Vamos a localizar los sensores de la  temperatura  como se muestra en la figura y hacer un complot para ellos en Y = 0; 12,5; 25; 37,5 mm. En los puntos dados compararemos la Solución numérica. obtenido utilizando el Análisis AutoFEM con la solución analítica.

Después de llevar a cabo el siguiente cálculo se obtienen los siguientes resultados:

Tabla 1. Parámetros de malla de elementos finitos

Tabla 2. Resultado " temperatura "

 

Conclusiones:

El error relativo de la solución numérica. en comparación con la solución analítica de es Igual a 0,8% (en el eje de la placa). Observe que cuando se refina la malla, la convergencia de la solución numérica. a la Solución Analítica es más lenta si hay problemas con la radiación ya que el problema es no lineal.

Cuando la solución de un problema no lineal, no importa que se utilizan los elementos para el cálculo: lineal o cuadrática.

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

**

En el ciclo sobre el número de los términos en la serie se realizó la diferenciación y sustitucion de la cuarta potencia de la solución en lugar de segunda derivada y de cero en lugar de la primera derivada en la expresión final.

 

Lea más acerca de AutoFEM Térmico Analysis

autofem.com

Volver al índice