 |
 |
 |
 |
 |
 |
AutoFEM Analysis Deflexión de una placa circular bajo una carga uniformemente distribuida |  |
|
|
|
|
|
|
AutoFEM Analysis Deflexión de una placa circular bajo una carga uniformemente distribuida | |
Deflexión de una placa circular bajo una carga uniformemente distribuida
Consideremos una placa circular con el radio a y el espesor h. La placa se sujeta y se somete a una carga distribuida de manera uniforme con la intensidad q (véase la figura).
|
El modelo de elementos finitos de una placa circular fijada bajo una carga distribuida de manera uniforme (la desviación grande) |
Vamos a usar los siguientes datos inicial: el radio de la placa a es 0,25 m, el espesor de la placa de h es 0,005 m, la intensidad de carga q is 1E+05 Pa.
Propiedades de los materiales son E=2.1E+011yν= 0.28.
Vamos a usar la siguiente fórmula aproximada para calcular desplazamientos del centro de la placa:
,
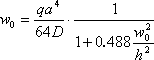Donde
es la rigidez a la flexión de la placa.
Resolviendo esta ecuación para W0, se obtiene el valor de la deflexión máxima, que se espera en el centro de la placa: w0= 2.3258E-003 m.
Después de la realización de los cálculos (teniendo en cuenta la no linealidad) por el Análisis AutoFEM se obtienen los siguientes resultados:
1.Parámetros Tabla de la malla de elementos finitos
Tipo de elementos finitos. |
Número de Nodos |
Número de elementos finitos. |
tetraedro cuadrática |
3000 |
8720 |
Tabla 2. Los resultados "Desplazamiento, magnitud"
Solución numérica. |
Solución analítica |
Error δ =100%*|w0*- w0|/| w0 | |
2.2938E-003 |
2.3258E-003 |
1.38 |
|
Conclusiones:
El error relativo de la solución numérica. en comparación con la solución analítica de es Igual a 1,38% para los elementos finitos cuadráticas.
* La numéricos Resultadosof pruebas dependen del elemento finito meshymay difieren ligeramente de los que figuran en las tablas.
Lea más acerca de AutoFEM Static Analysis
