Temperatura campo no estacionaria en un cilindro isotrópico

Vamos a considerar un problema de enfriamiento de un cuerpo cilíndrico con propiedades isotrópicas que tiene una temperatura inicial de t0=60 °C dentro del volumen. La Temperatura igual a cero se mantiene en el límite del cuerpo; tiempo de enfriamiento no exceda de 20 seg. Vamos a determinar la Temperatura en los puntos de control 1, 2, 3, que tienen las siguientes coordenadas en el sistema cilíndrico (el origen del sistema de coordenadas se encuentra en el centro del cilindro) de coordenadas: r1=25 mm, h1=25 mm; r2=25 mm, h2= - 25 mm; r3=30 mm, h3=0 mm en los siguientes momentos de tiempo t1,2,3=2; 10; 20 seg.

Parámetros de geométrica y física del cuerpo: altura del cilindro H = 100 mm, radio del cilindro a =50 mm. Densidad ρ=7700 kg/m3, calor específico c =460 J / (kg •°C), conductividad térmica K = 40 W / (m • °C). (ver la figura).

Busquemos la solución en el sistema de coordenadas cilíndricas. El centro del sistema de coordenadas está situado en el centro del cilindro en la sección transversal media (la altura total - h), y el eje de la que se mide la distancia (radio en el sistema de coordenadas cilíndrico - r) coincide con la eje del cilindro. Denotemos l = H / 2. A continuación, la solución de la ecuación toma la forma:

 

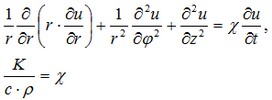
Condiciones de frontera para esta ecuación tienen el siguiente formulario:

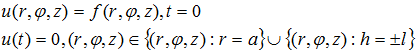
En las condiciones de contorno damos a entender que f - alguna distribución de la Temperatura en el interior del cuerpo en el momento inicial de tiempo, u (t) = 0 en la superficie del cuerpo cilíndrico durante todo el período de tiempo. Nos damos cuenta de que en nuestro caso f - es una constante.

Representamos la solución de la ecuación dada en la forma de una serie de funciones armónicas y de Bessel para el caso más general cuando f no es una constante.

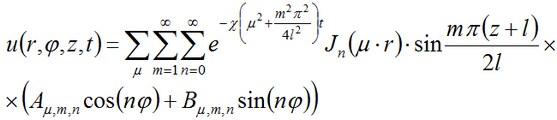
Donde χ=K/(c • ρ) el coeficiente de conductividad de temperatura, Jn (r) – función de Bessel, parámetro μ es una raíz de la ecuación Jn (a μ) =0

Los coeficientes AyB se puede calcular de acuerdo a las fórmulas que se muestran a continuación:

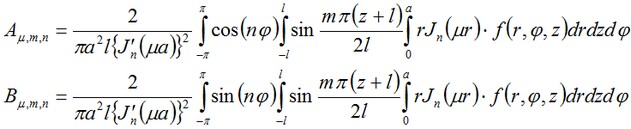
En nuestro caso simple cuando f = t0 de toda la serie sobre n tenemos sólo el primer término a la izquierda correspondiente a n=0. Pero la expansión en m y μ debe ser considerado. La forma simplificada de la solución se puede escribir como:

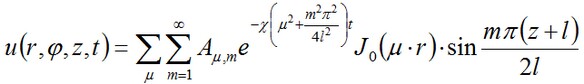
Donde

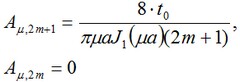
i.e.,  En la suma sobre m retenemos sólo los coeficientes impares.

Vamos a comparar el valor de la Temperatura en un punto fijo en diferentes momentos del tiempo con la solución obtenida por el método de los elementos finitos. El punto se seleccionará a una distancia suficientemente grande desde el eje principal del cilindro, para una mejor convergencia de la serie en la analítica Solución (la ecuación tiene una singularidad del tipo 1 / R que afecta significativamente la convergencia de la serie de Bessel funciones).

En los puntos dados compararemos la Solución numérica. obtenido utilizando el Análisis AutoFEM con el semi-analítico de uno en los momentos del tiempo: 2, 10, 20 seg.

 

Dado que la solución alternativa se obtuvo por el método semi-analítica (por extracción de las sumas parciales de la serie), que se requiere para determinar el número de dígitos significativos que se puede utilizar para la comparación con Solución analítica. Tabla que figura a continuación muestra con exactitud lo que los cálculos se llevaron a cabo para la obtención de la solución por la expansión de la serie y para la construcción de la trama solución. Conclusión sobre el número de dígitos significativos en la analítica Solución puede ser hecha por el indicador del cambio relativo en la solución y el hecho de que nuestra serie siempre converge.

Después de llevar a cabo el cálculo se obtienen los siguientes resultados:

Tabla 1. Parámetros de malla de elementos finitos

 

Tabla 2. Parámetros de tiempo de discretización

Tabla 3. Resultado "Temperatura"

 

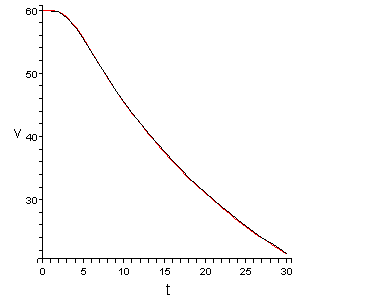
Conclusiones:

 

El error relativo de la solución numérica. en comparación con la analítica Solución es menor que 0,9% en 20 s. El error de cálculo es estable en el tiempo y no crece significativamente cuando se aumenta el tiempo de cálculo. Parcela de la dependencia de temperatura en tiempo muestra que numéricas analíticas y soluciona prácticamente coincidieron. El método resulta ser eficaz para la solución de los problemas con geometría compleja.

Al utilizar elementos cuadráticos el, Número de Nodos es significativamente mayor que para los elementos lineales. Por lo del tanto, con el tiempo (para cada nueva capa de tiempo), los elementos de segundo grado se acumulan error más grande que los elementos lineales. Como se puede ver, en 20 segundos, es decir, para el intervalo de tiempo relativamente pequeña para nuestro problema, elementos cuadráticos son más precisos que los elementos lineales, pero en el intervalo de tiempo significativamente más grande el error de cálculo con elementos cuadráticos se hizo aún más grande.

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

 

Lea más acerca de AutoFEM Térmico Analysis

autofem.com

Volver al índice