Temperatura  no estacionaria en el campo de una esfera isotrópica

Consideremos un problema de la determinación de un campo de  temperatura  en el interior de una esfera isotrópica en el volumen de lo que prescribimos la inicial  temperatura Tiinicial=293.15 oK,y que se calienta a lo largo de la superficie externa  donde prescribimos la  temperatura  constante Tperimétrica=373.15 oK (por ejemplo, la esfera en la sala  temperatura  fue sofocada al agua hirviendo). Vamos a determinar la temperatura en cualquier punto de la esfera (que se encuentra a una distancia r desde el centro de la esfera) en incrementos de tiempo iguales a Δt1,2,3 = 10, 20, 30 segundos.

 

La esfera tiene los siguientes parámetros: a = radio de 100 mm, la densidad del material 7800 kg / m3, calor específico c = 440 J / (kg •oK),  conductividad térmica K=50 W / (m • oK). Varias aleaciones de acero tienen características similares térmico.

Para la modelización numérica se considera una pieza de 1/8o de toda la esfera. Condiciones de simetría se hacen cumplir con la prescripción de cero flujo de calor en las superficies límite de la esfera que tienen un centro de la esfera como un vértice*2.

(ver la figura).

v dejara ser la solución deseada (campo de Temperatura). Entonces, teniendo en cuenta que la solución no depende de los ángulos de rotación del vector que emana desde el centro de la esfera (condición de simetría), podemos realizar el cambio de variables en la forma v=r•u, donde r – Distancia del centro. de la esfera,y u – alguna función. Después de este cambio de variables, se obtiene la ecuación para u:

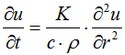
Donde t – es tiempo de enfriamiento / calentamiento del cuerpo sólido. Condiciones de frontera para u:

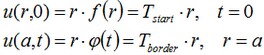
Por la solución de este problema por el método de separación de variables, se obtiene la expresión para v:

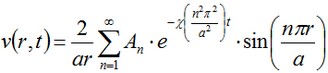
Donde χ=K/(c•ρ) es el coeficiente de conductividad Temperatura. Los pesos An en la expansión son determinados por la fórmula:

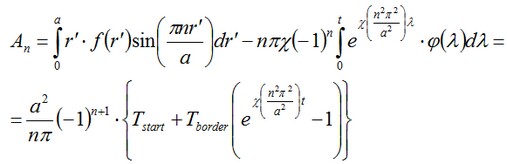
Comparemos la Solución numérica. con los obtenidos analítica semi-solución en el punto con radio R1 = 0,5 m.

En el punto dado compararemos la Solución numérica. obtenido utilizando el Análisis AutoFEM con el semi-analítico.

 

Dado que la solución alternativa se obtuvo por el método semi-analítica (por extracción de las sumas parciales de la serie), que se requiere para determinar el número de dígitos significativos que se puede utilizar para la comparación con Solución analítica. Tabla que figura a continuación muestra con exactitud lo que los cálculos se llevaron a cabo para la obtención de la solución por la expansión de la serie y para la construcción de la trama solución. Conclusión sobre el número de dígitos significativos en la solución analítica puede ser hecha por el indicador del cambio relativo en la solución y el hecho de que nuestra serie siempre convergentes.

Después de llevar a cabo el cálculo se obtienen los siguientes resultados:

Tabla 1. Parámetros de malla de elementos finitos

 

Tabla 2. Parámetros de tiempo de discretización

Tabla 3. Parámetros de cálculo de semi-Solución analítica obtenida por expansión de la serie

Para el cálculo numérico tomamos la resultados con N = 7000. Para la construcción de parcelas usamos la resultados con N = 500.

Tabla 4. Resultado "temperatura"

 

 

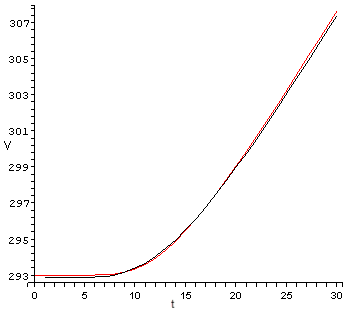
Conclusiones:

Obtuvimos imagen realista del campo temperatura. El error relativo de la solución numérica. en comparación con la solución analítica no exceda del 0,07% con elementos lineales en t = 30 s. El error de cálculo es estable en el tiempo y no crece significativamente cuando se aumenta el tiempo de cálculo. Parcela de la dependencia de temperatura en tiempo muestra que numérica.s analíticas y solución prácticamente coincidieron.

El error de cálculo con elementos cuadráticos es menor que con los elementos lineales en un pequeño intervalo de tiempo

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

**Por límites de Donde no se especifican las condiciones de frontera, el estado de flujo de calor cero se cumple automáticamente.

 

Lea más acerca de AutoFEM Térmico Analysis

autofem.com

Volver al índice