 |
AutoFEM Analysis Esfera hueca irradiando hacia fuera | ||||||
Esfera hueca irradiando hacia fuera
Consideremos un problema de la determinación del campo temperatura de estado estacionario de la esfera hueca, en la superficie interna de los cuales mantenemos una temperatura constante T1 =600 oK, y la superficie externa irradia al entorno ambiental. El entorno circundante tiene la temperatura Tamb=290 oK. Por esta temperatura el efecto de la radiación cambia significativamente la temperatura en el interior del volumen del cuerpo. Podemos determinar el campo temperatura en los puntos de control con los radios R123.
Características de la esfera: radio externo R = 100 мм; radio R interna / 2 = 50 mm; la Térmico conductividad K = 50 W / (m • OK); emisividad de la superficie esférica es Igual a α=1.
Consideremos una pieza 1/8o de toda la esfera. En las superficies laterales de la esfera prescribimos el flujo de calor cero. (ver la Figura).
|
Dado que el material es isotrópico, solución del problema dependerá sólo en el radio. Si el origen del sistema de coordenadas esféricas se coloca en el centro de la esfera, obtendremos la ecuación con condiciones de contorno:
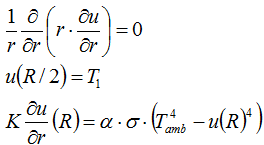
La solución de la ecuación tiene la forma:
![]()
Donde las constantes C1yC2 se determina a partir de las condiciones de contorno de la siguiente manera:
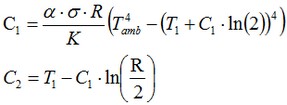
La primera ecuación (para los parámetros dados) tiene dos raíces reales. Para las raíces: C1 = -4483.400605yC2 = -12831.06789la solución en el límite tiene el negativo de temperatura en el límite. Para la escala Kelvin es imposible. Por lo tanto, sólo las raíces C1 = -13.02949201 y C2 = 560.9671302 satisfacen esta ecuación.
Comparemos la Solución numérica. con la Analítica solución obtenida en puntos con radio R123=0.0707106; 0.0848528; 0.0989949 m (coordenadas de los sensores en estos puntos: X123=50; 60; 70 mmyY123=50; 60; 70 mm).
En los puntos dados compararemos la Solución numérica. obtenido utilizando el análisis AutoFEM con la solución analítica.
|
|
El modelo de elementos finitos con condiciones de frontera aplicados |
Después de llevar a cabo el cálculo de los siguientes resultados se obtienen:
Tabla 1. Parámetros de malla de elementos finitos
Tipo de elementos finitos. |
Número de Nodos |
Número de elementos finitos. |
Tetraedro lineal |
2302 |
9830 |
Tabla 2. Resultado " temperatura "
Radius r, mm |
Solución numérica. |
Solución analìtica |
Error δ = 100%* |T* - T| / |T| |
0.0707106 |
585.7874 |
595.4843221 |
1.62 |
0.0848528 |
588.2587 |
593.1087648 |
0.81 |
0.0989949 |
591.6624 |
590.9686443 |
0.11 |
|
Conclusiones:
El error relativo de los cálculos se aproxima a 1,62%. Observe que cuando se refina la malla, la Solución numérica. se aproxima a la Solución Analítica más lento debido a la no linealidad del problema en sí.
Como vemos, al calcular la radiación, el error relativo es prácticamente el mismo para los elementos lineales y cuadráticas. Esto puede explicarse por el error en la solución de las ecuaciones no lineales. A si, al calcular la radiación, tiene sentido utilizar sólo elementos lineales debido al coste computacional menor.
El Resultados de pruebas numéricas depende de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.
** Las raíces se encontraron con la ayuda del sistema de arce 9.5.
Lea más acerca de AutoFEM Térmico Analysis