Placa ortotrópico de  grafito bajo un constante estado régimen de  temperatura

Consideremos ahora el problema de la distribución del campo  temperatura  estado estacionario para una placa con ortotrópicos conductividades térmico de un material cristalino a uno de los bordes de la cual se mantiene a una  temperatura  constante  Т1,y los bordes restantes son en Т2.

Como ejemplo, consideremos una placa de grafito rectangular con la conductividad térmico de K1=278 W/(m • oK) a lo largo de la dirección y principio K2=139 W/(m • oK) en una dirección perpendicular. Las dimensiones son: 200 mm х 100 mm. Los parámetros son a = 200 mm, b = 100 mm. La placa es alargado a lo largo de la dirección principio. Apliquemos la  temperatura  de T = 353,15 oK a uno de los bordes de un tamaño más pequeño. En el régimen de estado estacionario de la   temperatura es constante y no dependen del tiempo. La  temperatura  de 273,15 o K se aplica al resto de los bordes. Sobre toda la superficie (de ambos lados) un intercambio de calor con el entorno ambiental se lleva a cabo. La  temperatura  del medio ambiente es de 273,15 oK, el coeficiente de transferencia de calor es H=400 W/(m2 • oK). El espesor de la placa es D = 2 mm. (ver la Figura).

Para el problema dado, la ecuación diferencial tiene la forma:

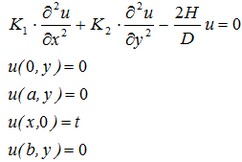
Este problema puede ser resuelto en el plano OXY-coordinar, en un dominio rectangular [0, a] х [0, b], asociado con la placa de grafito.

Solución analítica del problema se expresa en términos de series de Fourier y tiene la forma:

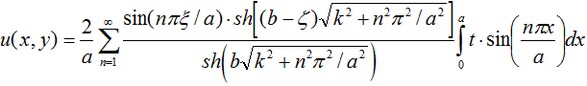
Las líneas ISOTERMICO de la solución obtenida tiene la forma mostrada en la Figura (obtenido con Arce 9.5):

Vamos a localizar los sensores de la  temperatura  como se muestra en la figura y hacer un complot para ellos en x = 50 mm, y = 10,20,30, ... 60 mm. En los puntos dados compararemos la solución numérica. obtenido utilizando el Análisis AutoFEM con la solución analítica.

Vamos a localizar los sensores de la  temperatura  como se muestra en la Figura y crea un complot para ellos en x = 50 mm, y = 10,20,30, ... 60 mm. En los puntos dados compararemos la solución numérica. obtenido utilizando el Análisis AutoFEM con la solución analítica.

Tabla 1. Parámetros de malla de elementos finitos

Tabla 2. Resultado " temperatura "

 

 

Conclusiones:

El error relativo de la solución numérica. en comparación con la solución analítica no exceda del 0,02% para los elementos lineales.

El presente método ha demostrado ser eficaz en la resolución de los problemas con la distribución anisotrópica de  temperatura s. La existencia de propiedades ortótropos no afecta a la eficiencia computacional del método.

La trama de la dependencia de la  temperatura  de la distancia indica que las numéricas solución y analíticos coincidieron desde un punto de vista práctico. Esto implica que las distribuciones de  temperatura  máximos mínimos Y son idénticos, y Por lo Tanto, el cálculo del flujo de calor y de energía se llevará a cabo con el mismo grado de precisión.

Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.

 

 

Lea más acerca de AutoFEM Térmico Analysis

autofem.com

 

Volver al índice