 |
 |
 |
 |
 |
 |
AutoFEM Analysis Punto de la fuente de alimentación dentro de la esfera |  |
|
|
|
|
|
|
AutoFEM Analysis Punto de la fuente de alimentación dentro de la esfera | |
Punto de la fuente de alimentación dentro de la Esfera
Consideremos un problema de encontrar un campo temperatura dentro de la esfera isotrópico con una fuente de punto en el centro. La temperatura se mantiene constante en la superficie esférica.
Radio de una esfera que delimita el cuerpo es de R = 0,1 m; la temperatura en la superficie de una esfera es t = 293,15 o K. El centro de la esfera coincide con el origen del sistema de coordenadas. Supongamos que en el centro de la esfera de una fuente puntual de calor de poder ρ=500 W se prescribe. Coordenadas del hijo fuente puntual Iguales un P0 = (0, 0, 0). Térmico conductividad se le asigna el valor igual a λ=1 W/(m•oK). [nuevo material con conductividad térmico = 1].
Para el modelado consideramos una parte 1/8th de la esfera. En el modelo numérico se aplica la potencia de 500 W, Y asi que dividirlo por 8, i.e., 500 / 8 = 62.5 W.
(ver la figura).
|
Para un problema dado una solución exacta en el punto P=P(x, y, z)se puede encontrar como:
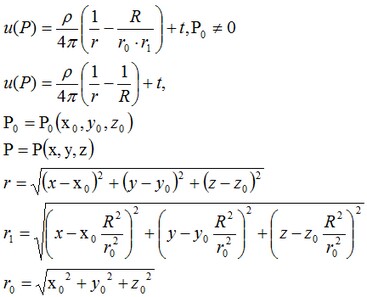
La función u es una solución de la ecuación diferencial y se puede escribir en la forma:
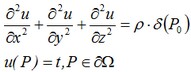
Donde δ es dira c δ-función, Ω – dominio de la esfera, ∂Ω – límite de la esfera.
|
|
El modelo de elementos finitos con condiciones de frontera aplicados |
Comparemos Solución analítica con la solución obtenida a partir de AutoFEM. Después de llevar a cabo el cálculo se obtienen los siguientes resultados:
Tabla 1. Parámetros de malla de elementos finitos
Tipo de elementos finitos. |
Número de Nodos |
Número de elementos finitos. |
Tetraedro lineal |
1370 |
6110 |
Tabla 2. Resultado " temperatura "
Distancia del centro., mm |
Solución numérica. |
Solución analítica |
Error δ = 100%* |T* - T| / |T| |
R 30 |
1243.813 |
1221.553 |
1.82 |
R 40 |
900.577 |
889.981 |
1.19 |
R 50 |
693.504 |
691.037 |
0.36 |
R 60 |
560.904 |
558.408 |
0.45 |
|
Conclusiones:
El error relativo de la solución numérica. en comparación con la solución analítica no excederá del 1,9% para los elementos lineales.
El método ha demostrado ser eficaz para la solución de problemas con las fuentes de punto y singularidades en la solución.
Además, tenga en cuenta que cerca de fuentes singulares (concentradas en el borde o en el punto), el error relativo es mayor que en los puntos más alejados de las fuentes. Esto sucede porque la temperatura en estas fuentes es Igual a infinito.
Los resultados de pruebas numéricas dependen de la malla de elementos finitos y pueden diferir ligeramente de los que figuran en la tabla.
Lea más acerca de AutoFEM Térmico Analysis
