 |
AutoFEM Analysis Axial Vibration Frequency and Transverse Vibration Frequency of the Beam with the Weight | ||||||
 |
AutoFEM Analysis Axial Vibration Frequency and Transverse Vibration Frequency of the Beam with the Weight | ||||||
Fréquence de vibration axiale et transversale d'une poutre avec un poids
Considérons la poutre en porte à faux, l'extrémité droite de ce qui est sous le poids.
|
La longueur de la poutre est L. La section transversale de la poutre est un rectangle de largeur b et de hauteur h. La masse du poids est M. La masse spécifique de la poutre est m.
m = ρ F,
où F = b h, ρ est la masse volumique du matériau de la poutre.
|
Le modèle éléments finis avec des charges et des contraintes |
Soit L est égale à 0,5 m, b est égal à 0,02 m, h est égal à 0,05 m.
Les propriétés du matériau sont: le module d'Young E = 2.1E+011 Pа, coefficient de Poisson ν=0.28, la densité ρ = 7800 kg / m3.
La masse de poids M est égal à 2.m.L kg (i.e. 7.8 kg).
Solution analytique of this problem is given by the following formulas:
a) la fréquence de vibration axiale
![]()
b) la fréquence de vibration transversal
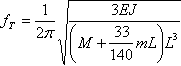 ,
,
![]() .
.
Donc, fA = 1078.962 Hz , fT = 22.092 Hz.
Après avoir effectué le calcul à l'aide de AutoFEM, les résultats suivants sont obtenus:
Tableau 1. Paramètres de maillage éléments finis
Type d'élément fini |
Nombre de nœuds |
Nombre d'éléments finis |
tétraèdre quadratique |
2173 |
8719 |
Tableau 2. Résultat "Fréquence"*
Solution numérique |
Solution analytique |
Erreur δ = 100%*| fi* - fi| / | fi | |
22.235 |
22.092 |
0.65 |
1080.013 |
1078.962 |
0.002 |
|
|
*Les résultats des tests numériques dépendent du maillage éléments finis et peuvent différer légèrement de celles indiquées dans le tableau.
En savoir plus sur AutoFEM Frequency Analysis